正十二面體

正十二面體

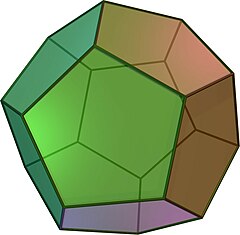(按這裏觀看旋轉模型)
類別	柏拉圖立體 正多面體
對偶多面體	正二十面體
識別
名稱	正十二面體
參考索引	U23, C26, W5
鮑爾斯縮寫	doe
數學表示法
施萊夫利符號	{5,3}
威佐夫符號	3 | 2 5
康威表示法	D
性質
面	12
邊	30
頂點	20
歐拉特徵數	F=12, E=30, V=20 （χ=2）
二面角	116.56505° = arccos(-1/√5)
組成與佈局
面的種類	正五邊形
面的佈局	12個{5}
頂點圖	5.5.5
對稱性
對稱群	Ih
特性
正凸多面體
圖像
5.5.5 （頂點圖） （展開圖）

正十二面體是由12個正五邊形所組成的正多面體，它共有20個頂點、30條棱、160條對角線，被施萊夫利符號{5,3}所表示，與正二十面體互成對偶。它是一種只具有正四面體對稱性的五角十二面體的特殊形式，五角十二面體的另一種特殊形式是具有正八面體對稱性的卡塔蘭多面體菱形十二面體，它（加上所有其它的五角十二面體）都與正十二面體在拓撲上等價。正十二面體還是截頂五方偏方面體的特例。其四維類比為正一百二十胞體。

十二面體

正十二面體是正二十面體的對偶多面體。

性質

面的圖形：正五邊形
面的數目：12
邊的數目：30
頂點數目：20
二面角角度：${\boldsymbol {\theta }}=\arccos \left(-{\frac {1}{\sqrt {5}}}\right)=2\arctan \varphi \approx 116.5650512^{\circ }$
如果正十二面體棱長為a：
表面積：$A=3{\sqrt {25+10{\sqrt {5}}}}a^{2}\approx 20.645728807a^{2}$
體積：$V={\frac {1}{4}}(15+7{\sqrt {5}})a^{3}\approx 7.6631189606a^{3}$
外接球半徑：$r_{u}=a{\frac {\sqrt {3}}{4}}\left(1+{\sqrt {5}}\right)\approx 1.401258538\cdot a$
內切球半徑：$r_{i}=a{\frac {1}{2}}{\sqrt {{\frac {5}{2}}+{\frac {11}{10}}{\sqrt {5}}}}\approx 1.113516364\cdot a$
中分球半徑：$r_{m}=a{\frac {1}{4}}\left(3+{\sqrt {5}}\right)\approx 1.309016994\cdot a$

• 我們亦可以將上述三式寫作：

外接球半徑：$r_{u}=a\,{\frac {\sqrt {3}}{2}}\varphi$

內切球半徑：$r_{i}=a\,{\frac {\varphi ^{2}}{2{\sqrt {3-\varphi }}}}$

中分球半徑：$r_{m}=a\,{\frac {\varphi ^{2}}{2}}$

（在這裏φ是黃金分割數，φ = ^1+√5/₂）

• 注意到棱長為a的正十二面體的外接球同樣外接於棱長為φa的立方體，並且其內切球半徑（也即面心距）等於棱長為φa的正五邊形的邊心距。

對偶多面體：正二十面體

坐標系

頂點坐標：
	橙色的頂點位於(±1, ±1, ±1)，形成了其一個內接立方體(虛線所示)。
	綠色的頂點位於(0, ±φ, ±1/φ)，形成了y–z平面上的一個矩形。
	藍色的頂點位於(±1/φ, 0, ±φ)，形成了x–z平面上的一個矩形。
	粉色的頂點位於(±φ, ±1/φ, 0)，形成了x–y平面上的一個矩形。
相鄰頂點間的距離是2/φ，頂點到原點的距離是√3. φ = (1 + √5) / 2是黃金分割數。

如果我們以正十二面體的形心為原點建立三維直角坐標系，那麼其20個頂點可被描述為：
(0,±φ,±1/φ)
(±1/φ,0,±φ)
(±φ,±1/φ,0)
(±1,±1,±1)
其中φ = (1+√5)/2，是黃金分割數，也被寫作τ，約等於1.618。
該正十二面體棱長為²/_φ=√5–1。其外接球半徑正好為√3。

二維投影和對稱性

正十二面體有兩種特殊的正交投影，分別正對着其一個頂點和一個正五邊形面，對應着A₂和H₂考克斯特平面

正交投影

正對於	頂點	棱	面
圖像
投影 對稱性	[[3]] = [6]	[2]	[[5]] = [10]

在透視投影中，如果如果投影中心正在正十二面體外接球正對其一面的一點，則你能得到其施萊格爾圖像，我們亦可以將其視為球面多面體而使用球極投影。這些方法也被用於可視化其四維類比正一百二十胞體，一個由120個全等的正十二面體組成的四維凸正多胞體。

投影	正交投影	透視投影
		施萊格爾圖像	球極投影
正十二面體
正120胞體

幾何關聯

• 正十二面體是一個無窮家族——截對角偏方面體的第3個成員（截對角五方偏方面體）。這類多面體可以被看作是將偏方面體在旋轉對稱軸上的兩個相對的頂點截去而成。
• 正十二面體的星形化體構成了4個星形正多面體中的3個。
• 我們可以在正十二面體的20個頂點中選取5組這樣的頂點，使任意兩個頂點的連線都是正十二面體正五邊形面的一條對角線，這樣能構成正十二面體的內接立方體，5個內接立方體一起構成了——複合多面體——五複合立方體；我們還可以進一步對內接立方體做交錯操作，得到正十二面體的內接正四面體，如果我們只在內接立方體中取一個正四面體，則5個正四面體構成了有手征性的複合多面體——五複合四面體；如果取兩個，則10個正四面體構成了複合多面體——十複合四面體，這三個複合多面體都是正十二面體的小面化體。
• 正十二面體的完全對稱群是正二十面體對稱群I_h，考克斯特群[5,3]，群階120，還有一個抽象群結構A₅×Z₂。

與其對偶——正二十面體的關係

• 當正十二面體和正二十面體內接於同一球時，儘管正二十面體有更多的面，但正十二面體佔據球的體積（66.49%）要多於正二十面體佔據的球的體積（60.54%），這一點與二維不同。
• 棱長相同為1的正十二面體的體積（7.663...）是正二十面體體積（2.181...）的三倍半多。

相關多面體

正十二面體在拓撲上與一系列三階正鑲嵌（頂點圖為n³）有關：

多面體				歐式鑲嵌	雙曲鑲嵌
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	...	{∞,3}

正十二面體在拓撲上還和其它階的正五邊形正鑲嵌{5,n}(n≥3)有關：

多面體		歐式鑲嵌	雙曲鑲嵌
{5,2}	{5,3}	{5,4}	{5,5}	{5,6}	{5,7}	{5,8}	...	{5,∞}

正十二面體可以通過不同類型的截取操作來得到一系列不同的半正多面體及其對偶，正二十面體，構成了正二十面體家族：

正二十面體家族半正多面體

對稱群: [5,3], (*532)							[5,3]+, (532)
{5,3}	t0,1{5,3}	t1{5,3}	t0,1{3,5}	{3,5}	t0,2{5,3}	t0,1,2{5,3}	s{5,3}
半正多面體對偶
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

頂點分佈

正十二面體與4個星形半正多面體和上述3個複合半正多面體有同樣的頂點分佈：

大星形十二面體	小雙三斜三十二面體	雙三斜二十四面體	大雙三斜三十二面體
五複合立方體	五複合四面體	十複合四面體

星形化體

正十二面體的3個星形化體都是星形正多面體（開普勒-普索多面體）：

	0	1	2	3
星形化體	正十二面體	小星形十二面體	大十二面體	大星形十二面體
表面圖形

倒角多面體

類別	柏拉圖立體					卡塔蘭立體
種子	{3,3}	{4,3}	{3,4}	{5,3}	{3,5}	aC	aD
倒角	cT	cC	cO	cD	cI	caC	caD

相關數學問題

• 哈密頓路徑的理論就是源自一個和正十二面體有關的問題：試求一條路徑，沿正十二面體的棱經過它所有的頂點。

應用

• 因為一年有12個月，正十二面體正好用來製作月曆。
• Pariacoto virus的形狀結構是正十二面體。
• 在英國到匈牙利，至到意大利東部等地，找到過百個形狀接近十二面體、以銅或石頭製造的空心物件。它們被稱為Dodecaeder，用途不明。
• 五魔方（Megaminx）就是正十二面體製作出來的魔方。

正十二面烷

化學：

• 硫化鐵結晶體有時會出現接近正十二面體的形狀。
• 最小的富勒烯C₂₀結構如正十二面體。
• 正十二面體烷C₂₀H₂₀是個人工合成的碳氫化合物

參考文獻

1. 埃里克·韋斯坦因. Dodecahedron. MathWorld. 
2. 埃里克·韋斯坦因. Elongated Dodecahedron. MathWorld. 
3. Klitzing, Richard. 3D convex uniform polyhedra o3o5x – doe. bendwavy.org. 
4. Editable printable net of a dodecahedron with interactive 3D view （頁面存檔備份，存於互聯網檔案館）
5. The Uniform Polyhedra （頁面存檔備份，存於互聯網檔案館）
6. Origami Polyhedra （頁面存檔備份，存於互聯網檔案館） – Models made with Modular Origami
7. Dodecahedron （頁面存檔備份，存於互聯網檔案館） – 3-d model that works in your browser
8. Virtual Reality Polyhedra （頁面存檔備份，存於互聯網檔案館） The Encyclopedia of Polyhedra
   • VRML models
   1. Regular dodecahedron （頁面存檔備份，存於互聯網檔案館） regular
   2. Rhombic dodecahedron （頁面存檔備份，存於互聯網檔案館） quasiregular
   3. Decagonal prism （頁面存檔備份，存於互聯網檔案館） vertex-transitive
   4. Pentagonal antiprism （頁面存檔備份，存於互聯網檔案館） vertex-transitive
   5. Hexagonal dipyramid （頁面存檔備份，存於互聯網檔案館） face-transitive
   6. Triakis tetrahedron （頁面存檔備份，存於互聯網檔案館） face-transitive
   7. hexagonal trapezohedron （頁面存檔備份，存於互聯網檔案館） face-transitive
   8. Pentagonal cupola （頁面存檔備份，存於互聯網檔案館） regular faces
9. K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra （頁面存檔備份，存於互聯網檔案館）
10. Dodecahedron 3D Visualization （頁面存檔備份，存於互聯網檔案館）
11. Stella: Polyhedron Navigator （頁面存檔備份，存於互聯網檔案館）: Software used to create some of the images on this page.

外部連結

• 埃里克·韋斯坦因, 正十二面體 （參閱柏拉圖立體） 於MathWorld（英文）