跳转到内容

惯性

本页使用了标题或全文手工转换
维基百科，自由的百科全书

在物理学里，惯性（英语：inertia）是物体抗拒其运动状态被改变的性质。物体的惯性可以用其质量来衡量，质量越大，惯性也越大。艾萨克·牛顿在钜著《自然哲学的数学原理》里定义惯性为：[1]

惯性，或物质固有的力，是一种抗拒的现象，它存在于每一物体当中，大小与该物体相当，并尽量使其保持现有的状态，不论是静止状态，或是匀速直线运动状态。

更具体而言，牛顿第一定律表明，存在某些参考系，在其中，不受外力的物体都保持静止或匀速直线运动。也就是说，从某些参考系观察，假若施加于物体的合外力为零，则物体运动速度的大小与方向恒定。惯性定义为，牛顿第一定律中的物体具有保持原来运动状态的性质。满足牛顿第一定律的参考系，称为惯性参考系。稍后会有关于惯性参考系的更详细论述。

惯性原理是经典力学的基础原理。很多学者认为惯性原理就是牛顿第一定律。遵守这原理，物体会持续地以现有速度移动，除非有外力迫使改变其速度。

在地球表面，惯性时常会被摩擦力、空气阻力等等效应掩蔽，从而促使物体的移动速度变得越来越慢（通常最后会变成静止状态）。这现象误导了许多古代学者，例如，亚里士多德认为，在宇宙里，所有物体都有其“自然位置”──处于完美状态的位置，物体会固定不动于其自然位置，只有当外力施加时，物体才会移动。[2]

历史

[编辑]

早期认知

[编辑]

文艺复兴之前，在西方哲学里最被广泛接受的运动理论是建立于大约公元前335年至公元前322年的亚里士多德的学说。亚里士多德表明，假设没有“暴力”（violent force）施加，所有（在地球上的）物体最终都会停止运动，静止于其自然位置，但只要有暴力促使物体运动，物体会持续其运动状态。当抛物体被抛掷出去时，抛掷者的暴力转移到抛物体周围的空气，使这些空气流动，成为新的推动者，继续不停地促使抛物体移动。[3][4]

在之后大约两千年内，亚里士多德的运动概念广泛地被接受，只有几位著名哲学家对这概念提出质疑。例如，在第6世纪，约翰·斐劳波诺斯严厉批评亚里士多德关于物体运动的不一致理论：亚里士多德认为真空不可能存在，因为，在真空里，没有任何介质促使物体移动，但是，他又表示，介质的阻力与其密度成正比：假设空气的密度是水的一半，则物体通过同样路径所用掉的时间，在空气中是在水中的一半，那么，物体通过真空所用掉得时间应该更少。[5]斐劳波诺斯主张，介质只能阻碍抛物体的运动，不能促使抛物体移动；在真空里，没有任何介质，抛物体反而比较容易移动。[6]斐劳波诺斯建议，促成抛物体持续运动的因素与周围介质无关，而是在运动刚开始时，加诸于抛物体的某种性质，这性质逐渐在运动时消耗殆尽。虽然这建议与当今惯性概念仍有所差异，至少它已朝着正确方向跨出基要的脚步。[7][4]但是，在那时期与之后很多年，他的想法没有得到重视，很多亚里士多德派学者都给予强烈反对，包括托马斯·阿奎那（约1225年－1274年）和艾尔伯图斯·麦格努斯（约1200年－1280年）在内。只有奥卡姆的威廉（约1288年－1348年）反对亚里士多德物理学。他质疑亚里士多德所提到的运动的“推动者”到底在哪里，虽然他否定亚里士多德公理的正确性，认为抛物体的运动不需要随时随地都有推动者伴随。但是，他也没能给出任何替代答案。[6]

冲力说

[编辑]
主条目：冲力说

在第14世纪，法国哲学家让·布里丹提出冲力说。他称呼促使物体运动的性质为冲力，这冲力是由推动者传送给物体，促使物体运动。他否定了冲力会自己消耗殆尽的想法。布里丹认为永存不朽的冲力是被空气阻力或磨擦力等等逐渐抵销，只要冲力大于阻力或磨擦力等等，物体就会继续移动。[8][9]布里丹的冲力与物体密度和体积成正比；速度越大，冲力也越大；物体内部的物质越多，就能够接受越多的冲力。[6]

从日常观察中，布里丹想出许多反例来反驳亚里士多德的理论：[6]

  • 假设一个陀螺或磨石绕着固定轴旋转，请问空气怎样在这些物体的后面推动旋转？
  • 现在，为这旋转物量身打造一个铸模，将这铸模包在旋转物外面，不让在旋转物与铸模之间有任何空隙。这样，在旋转物与铸模之间，不会存在任何空气，请问空气怎样推动旋转？
  • 设想一艘拖船拖拽著另一艘船，航行于风平浪静的静止大海。现在，将拖绳切断，则因为海水阻力与空气阻力，被拖的船会慢慢的停止航行。在这时候，站在甲板上、面向船前方的海员会感觉到空气对着脸面吹拂，从船前方吹向船后方，试图减慢船的航行；他不会感觉到空气对着后背吹拂，从船后方吹向船前方，试图推动船的航行。
  • 思考石头与羽毛这两种物质，空气应该比较容易推动羽毛。但是，为什么同样地分别将石头与羽毛抛射出去，石头移动的距离比羽毛远了很多？

尽管与惯性的现代概念很相似，布里丹只把自己的理论视为亚里士多德基本哲学的微小修正，坚持许多其他亚里士多德派的观念，例如，他认为运动状态与静止状态是两种不同的状态。布里丹又主张，冲力不但适用于直线运动，也适用于圆周运动，促使物体（例如，星体）呈圆周运动。[9]

萨克森的阿尔伯特（英语：Albert of Saxony (philosopher)）是布里丹的学生。他将布里丹的学说广传至意大利与中欧。[10][9]在牛津大学墨顿学院的思想家赫特斯柏立的威廉最先表述出平均速率定理：在同样时间间隔内，假若匀速度物体的速度是等加速度物体的最初速度和最终速度的总和的一半，则此二物体移动的距离相等。这定理是自由落体定律的基础。早在伽利略·伽利莱之前，他们就已做实验证实了这定理。[11]

尼克尔·奥里斯姆又将他们的研究结果加以发挥，他创立了用曲线图来解释运动定律的方法，并且用几何方法证明平均速度定理。奥里斯姆于1377年发表的著作《天地通论》提出，当自由落体在加速时，其重量并没有增加，而是冲力增加。假设，挖掘一条直线隧道，从地球表面的A点，穿过地心，挖掘到地球表面的B点，然后将一个重物落入这隧道，则它会从A点，经过地心，移动到B点，就好像单摆从一边摇摆到另外一边。但是，从地心到B点的路途中，它是呈升起状态，而重量只能造成物体掉落，因此冲力与重量不同。[12]

这些研究发展逐渐地侵蚀了学者们对于亚里士多德物理学的信心。[13]在伽利略发表惯性原理之前不久，于1585年，意大利物理学者乔望尼·本尼得棣将越加成熟的冲力说限制为只能适用于直线运动：[14]本尼得棣特别举出甩石机弦的例子，当旋转甩石机弦时，皮袋内的石头，由于被皮绳约束，原本的直线运动被迫变为圆周运动；但若将石头扔出，脱离皮绳的约束，则石头会呈直线运动，而石头的直线轨迹会正切圆周于扔出点。[15][16]

经典惯性

[编辑]

尼古拉·哥白尼于1543年发表著作《天体运行论》，主张地球（与处于其表面的所有物体）从未停止不动，而是持续地绕着太阳做公转。面对这崭新的理论，亚里士多德式的地心说──地球是宇宙的中心，因此绝对地固定不动──显得漏洞百出、难以招架。[17]在发表著作之前，哥白尼为了证实自己的理论，早已于1530年就完成了观测行星轨道运动的实验。[18]

德国天文学者开普勒，在从1618年至1621年分三阶段发表的著作《哥白尼天文学概要》里，最先提出术语“惯性”，拉丁语为“懒惰”的意思，与当今的诠释不太一样。开普勒以对于运动变化的抗拒来定义惯性，这仍旧是根据亚里士多德的静止状态为自然状态的前提。一直要等到后来伽利略的研究与牛顿将静止与运动统一于同一原理，术语惯性才能应用于当今其所赋有的概念。

伽利略用来检验惯性定律的斜面实验。

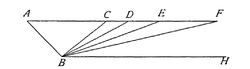
伽利略·伽利莱主张，施加外力改变的是物体的速度而不是位置；维持物体速度不变，不需要任何外力。为了证实他的主张，伽利略做了一个思想实验。如右图所示，让静止的小球从点A滚下斜面AB，滚到最底端后，小球又会滚上斜面BC，假设两块斜面都非常的平滑、摩擦系数极小，而且空气阻力微弱，以至于可以忽略不计，则小球会滚到与点A同高度的点C；假设斜面是BD、BE或BF，小球也同样地会滚到与点A同高度的位置。只不过斜面越长，往上滚的时候，单位时间内速度的减少量会变得越小。假设斜面逐渐延长，最后变成水平面BH，则基于“连续性原则”该小球“本应当”回到与点A同高度的位置，然而由于事实上BH是水平的，小球永远不可能滚到先前的高度，而速度的减少量将变成0，因此小球会不停地呈匀速直线运动。伽利略总结，假若不碰到任何阻碍，那么运动中的物体会持续地做匀速直线运动。他将此称为惯性定律[19][20]。

这理论刚被提出时并不被其他学者接受，因为当时大多数学者不了解摩擦力与空气阻力的本质，不过伽利略的实验以可靠的事实为基础，经过抽象思维，抓住主要因素，忽略次要因素，更深刻地反应了自然规律。

值得注意的是，后来，伽利略从惯性定律推论，假若没有任何外在参考比较，则绝对无法分辨物体是静止不动还是移动。这观察后来成为爱因斯坦发展狭义相对论的基础。[21]

好几位其他自然哲学家与科学家似乎分别独立地想出了惯性定律[注 1]。第17世纪哲学家勒内·笛卡儿也曾经提出惯性定律，虽然他没有做出任何实验来证实这定律的正确性。

牛顿第一定律其实正是伽利略所提出的惯性定律的再次陈述[22]──不施加外力，则没有加速度，因此物体会维持速度不变。牛顿将这定律的最初提出归功于伽利略。牛顿第一定律为[23]

物体会保持其静止或匀速直线运动状态，除非有外力迫使改变其状态。

写出牛顿第一定律后，牛顿开始描述他所观察到的各种物体的自然运动。像飞箭、飞石一类的抛体，假若不被空气的阻力抗拒，不被重力吸引坠落，它们会速度不变地持续运动。像陀螺一类的旋转体，假若不受到地面的摩擦力损耗，它们会永久不息地旋转。像行星、彗星一类的星体，在阻力较小的太空中移动，会更长久地维持它们的运动轨道。在这里，牛顿并没有提到牛顿第一定律与惯性参考系之间的关系，他所专注的问题是，为什么在一般观察中，运动中的物体最终会停止运动？他认为原因是有空气阻力、地面摩擦力等等作用于物体。假若这些力不存在，则运动中的物体会永远不停的做匀速运动。这想法是很重要的突破，需要极为仔细的洞察力与丰富的想像力才能达成。

相对论

[编辑]

阿尔伯特·爱因斯坦于1905年在论文《论动体的电动力学》里提出的狭义相对论，是建立于伽利略与牛顿研究出来的惯性与惯性参考系。尽管这划时代的理论实际地改变了许多牛顿概念，像质量、能量、距离，但爱因斯坦的惯性概念与牛顿的原本概念丝毫没有任何差异。实际而言，整个理论是建立于牛顿的惯性定义。但这也使得狭义相对论的相对性原理只能应用于惯性参考系。在这种参考系里，不受外力的物体，必定保持其静止或匀速直线运动状态。为了处理这局限，爱因斯坦于1916年发表论文《广义相对论的基础》提出广义相对论。这理论能够应用于非惯性参考系。但是，为了达到这目的，爱因斯坦发觉，他必需使用到弯曲时空的新概念，而不是传统的牛顿力的概念，来重新定义几个基础概念（例如重力）。

因为这重新定义，爱因斯坦还以测地误差重新定义了惯性的概念，这又引起一些微妙但重要的结果。根据广义相对论，当处理大尺寸问题时，不能使用与倚赖传统牛顿惯性。幸运地，对于足够小的时空区域，狭义相对论仍旧适用，惯性的内涵与工作仍旧与经典模型相同。

狭义相对论的另一个深奥的结果是，能量与质量不是互不相干的物理属性，而是可互相转换的。这崭新关系也给予惯性概念新的内涵。狭义相对论的逻辑结果是，假若质量遵守惯性原理，则能量必也遵守惯性原理。对于很多状况，这理论大大地拓宽了惯性的定义，能够应用于物质与能量。

诠释

[编辑]

质量与惯性

[编辑]

惯性的定性定义为物体抗拒动量改变的性质。将这定义加以定量延伸为物体抗拒动量改变的度量，就可以用来做数学计算。这度量称为惯性质量，简称为质量。所以，质量表示物质的数量，同时，质量也是物体惯性的度量。

动量方程表达物体的动量 与质量 、速度 之间的关系：

。

但是，牛顿第二定律方程也可以表达物体的作用力 与质量（惯性质量） 、加速度 之间的关系：

。

按照这个方程，给定作用力，则质量越大，加速度越小。由动量方程与牛顿方程给出的质量相同。因为，假若质量与时间、速度无关，则牛顿方程可以从动量方程推导出来。

这样，质量是物体惯性的度量，即物体抗拒被加速的度量。物体惯性这词语的含意，已从原本含意──维持动量的倾向，改变为物体抗拒动量改变的度量。

重力质量与惯性质量

[编辑]

重力质量与惯性质量之间的唯一差别是测量方法。

将未知质量的物体与已知质量的物体分别感受到的重力做测量比较，就可以得到未知物体的重力质量。通常，可以使用天平来做测量。这方法的优点是，不论在什么地方，在什么星球，都可以用天平来做测量，因为对于任意物体，重力场都一样。只要重力场不改变，天平会测量出可信的重力质量。但是，在超质量星体附近，例如，黑洞或中子星，就不能采用这种方法，因为在这区域里，重力场的梯度太过陡峭，在天平的左右两个托盘位置的重力场差异量太大，超过允许误差范围。在失重环境，也不能采用这种方法，因为天平不能做任何比较。

施加已知作用力于未知质量的物体，测量产生的加速度，然后应用牛顿第二定律方程，就可以得到惯性质量，其误差只限制于测量的准确度。当处于自由落体状况时，使用这方法，坐在一种特别座椅，称为物体质量测表，就可以测量出失重航天员的惯性质量。

值得注意的是，实验者尚未找出，重力质量与惯性质量，两者之间有什么差异。实验者已完成许多实验，检验两者的实验数值，但是差异都在实验误差边限之内。爱因斯坦在创建广义相对论时，从重力质量与惯性质量相等的事实，得到很大的启示。他假设重力质量与惯性质量相同，重力所产生的加速度是时空连续统内的斜度所造成的结果，就好像圆球以螺旋线样式滚下一个倒圆锥。

惯性参考系

[编辑]

当描述物体运动时，只有相对于特定的参考系，才能确实显示出其物理行为。假若选择了不适当的参考系，则相关的运动定律可能会比较复杂，在惯性参考系中，力学定律表现出的形式最为简单。[24]从惯性参考系观察，任何呈匀速直线运动的参考系，也都是惯性参考系，否则是“非惯性参考系”。换句话说，牛顿定律满足伽利略不变性，即在所有惯性参考系里，牛顿定律都保持不变[25]。

选择以固定星体来近似惯性参考系，这方法的误差相当微小。例如，地球绕着太阳的公转所产生的离心力，比太阳绕着银河系中心的公转所产生的离心力，要大三千万倍。所以，在研究太阳系中星体的运动时，太阳是一个很好的惯性参考系。[26]地球也可以视为惯性参考系。由于地球自转而产生的加速度在地球表面为0.034m· s-2。重力加速度大约为自转加速度的288倍。由于地球绕着太阳公转而产生的加速度为0.006m· s-2，更为微小。所以，可以忽略地球的自转和公转加速度。[27]

假设处于地球参考系的观察者A，观察到一辆火车呈匀速直线运动，则附着于此火车的参考系（火车参考系）也是惯性参考系。现在，在火车车厢内，有一个圆球从高处掉落下来，处于火车参考系的观察者B，所观察到的圆球轨迹，就如同当这火车固定不动时，这圆球会垂直掉落下来一样。从地球参考系观察，在掉落之前，圆球与火车的移动速度与方向相同，圆球的惯性保证，朝着火车移动方向，圆球与火车的移动速度相等。注意到在这里，是惯性而不是质量给出这保证。

每一个惯性参考系里的观察者，都会观察到所有物理行为都遵守同样的物理定律。从一个惯性参考系，可以简单又直觉明显地变换（伽利略变换）到另外一个惯性参考系。这样，处于地球参考系的观测者A能够推论，火车参考系的观察者B会观察到，在火车车厢内掉落的圆球，会垂直掉落下来。

对于非惯性参考系而言，由于参考系的加速度不等于零，物体会感受到虚设力。假设火车正在加速度中，则火车参考系的观察者B会观察到，圆球不会垂直地掉落，而会偏改方向，这是因为朝着火车移动方向，圆球与火车的移动速度不相等。

再举一个例子，假设将地球自转纳入考量，地球每24小时会自转一周，旋转的地球参考系是非惯性参考系。从北极发设一枚导弹，对准南方位于赤道的某点P，则从地球参考系观察，由于感受到科里奥利力，这枚导弹会偏离点P。但是，从太阳参考系观察，由于地球的自转，点P位置有所改变，所以没有准确抵达点P。

起源

[编辑]

牛顿特别定义绝对空间为不依赖于外界任何事物而独自存在的参考系，在绝对时空中，不受力的物体具有保持原来运动状态的性质，这性质称为“惯性”。牛顿认为惯性是物体的内秉性质。

恩斯特·马赫认为，绝对空间的概念太过玄秘，绝对空间不是可以实际观察测得。假若将所有遥远星体的运动平均，得到的参考系应该是静止的，可以替代绝对空间。因此，物体的惯性与遥远的星体有关，物体的惯性起源于其与整个宇宙的物质之间的相互作用，也就是说，“远域的物质决定了本域的惯性”。但是，远在宇宙的那一端，相距109光年宇宙半径的星球，怎么能够影响本域的惯性？尽管马赫的批评很有道理，牛顿力学的准确度是有眼共睹的事实。究竟是什么原因造成了远域的物质似乎与本域的惯性没什么牵连的表象？

爱因斯坦在研究广义相对论时，深深地被马赫的理论吸引与启发，爱因斯坦称这想法为马赫原理。爱因斯坦表明，重力是遥远物质影响本域惯性的机制，而这耦合发生于弯曲时空，可以用几何动力学的初值方程计算求得。根据爱因斯坦的理论，只要知道宇宙的整个质量－能量分布与流动，就可以计算出，在任意位置与时间，物体的惯性。这具体地给出了马赫定理的操作机制。[28]

假设一个旋转圆球壳的质量等于地球质量、半径等于地球半径、旋转角速度等于地球自转角速度，在圆心位置有一个傅科摆，则这旋转圆球壳对于傅科摆产生的参考系拖拽现象，与整个宇宙对于傅科摆产生的现象，两者之间的比率大约为5×10-14。因此，可以结论地球对于傅科摆的影响相当微小。假若地球质量加大0.2×1014倍，则旋转圆球壳对于傅科摆产生的参考系拖拽现象相当于宇宙对于傅科摆产生的现象。[28]

转动惯量

[编辑]
工业飞轮具有很大的转动惯量，可以用来抗拒转速的改变。当动力源对旋转轴作用有一个变动的力矩时（例如往复式发动机），或是应用在间歇性负载时（例如活塞或冲床），飞轮可以减小转速的波动，使旋转运动更加平顺。

转动惯量是惯性的另外一种形式，指的是刚体在旋转时维持其匀速旋转运动的倾向。除非有外力矩施加，刚体的角动量不会改变。这理论称为角动量守恒定律。由于陀螺仪的转动惯量，它可以抗拒任何对于旋转轴方向的改变。

参阅

[编辑]

注释

[编辑]
  1. ^ 英国政治哲学家托马斯·霍布斯在著作《利维坦》里这样陈述：

    当物体静止不动时，除非有什么事件将它搅动，它会永远静止不动。没有人会怀疑这真理。但是当物体在运动中，除非有什么事件将它停止，它会永远地运动。虽然理由相同（没有任何东西可以改变自己），这论点并不是很容易让人信服。

参考文献

[编辑]
  1. ^ Newton 1846，第72页
  2. ^ Pages 2 to 4, Section 1.1, "Skating", Chapter 1, "Things that Move", Louis Bloomfield, Professor of Physics at the University of Virginia, How Everything Works: Making Physics Out of the Ordinary, John Wiley & Sons (2007), hardcover, 720 pages, ISBN 978-0-471-74817-5
  3. ^ Aristotle, Physics, 8.10, 267a1-21; Aristotle, Physics, trans. by R. P. Hardie and R. K. Gaye 互联网档案馆的存档，存档日期2007-01-29..
  4. ^ 4.0 4.1 Darling, David, Gravity's arc: the story of gravity, from Aristotle to Einstein and beyond, John Wiley and Sons: pp. 17, 50, 2006 [2011-12-15], ISBN 9780471719892, （原始内容存档于2012-10-25） 
  5. ^ Dugas 1988，第20-21页
  6. ^ 6.0 6.1 6.2 6.3 Dugas 1988，第47-50页
  7. ^ Richard Sorabji, Matter, Space, and Motion: Theories in Antiquity and their Sequel, (London: Duckworth, 1988), pp. 227-8; Stanford Encyclopedia of Philosophy: John Philoponus. （页面存档备份，存于互联网档案馆）
  8. ^ Jean Buridan: Quaestiones on Aristotle's Physics (quoted at 存档副本. [2011-07-20]. （原始内容存档于2011-07-20）. )
  9. ^ 9.0 9.1 9.2 Glick 2005，第107页
  10. ^ Dales, Richard, The scientific achievement of the Middle Ages illustrated, University of Pennsylvania Press: pp. 111, 1973, ISBN 9780812210576 
  11. ^ Glick 2005，第222页
  12. ^ Dugas 1988，第59页
  13. ^ Glick 2005，第377页
  14. ^ Giovanni Benedetti, selection from Speculationum, in Stillman Drake and I. E. Drabkin, Mechanics in Sixteenth Century Italy University of Wisconsin Press, 1969, p. 156.
  15. ^ Drake, Stillman; Swerdlow, Noel; Levere, Trevor, Essays on Galileo and the history and philosophy of science, Volume 3 llustrated, University of Toronto Press: pp. 282, 285, 1999, ISBN 9780802081650 
  16. ^ Dugas 1988，第105页
  17. ^ Nicholas Copernicus: The Revolutions of the Heavenly Spheres （页面存档备份，存于互联网档案馆）, 1543
  18. ^ Dugas 1988，第84页
  19. ^ 马赫, 恩斯特, The science of mechanics; a critical and historical account of its development, Watchmaker Publishing: pp. 140–141, 2010 [1919], ISBN 978-1603863254 
  20. ^ Frautschi, Steven. The Mechanical universe: mechanics and heat illustrated. Cambridge University Press. 1986: pp.60–62. ISBN 9780521304320. 
  21. ^ Cropper, William, Great physicists: the life and times of leading physicists from Galileo to Hawking illustrated, Oxford University Press: pp. 206–207, 2004, ISBN 9780195173246 
  22. ^ Dugas 1988，第200-207页
  23. ^ Newton 1846，第83-93页
  24. ^ Landau, L. D.; Lifshitz, E. M. Mechanics. Pergamon Press. 1960: 4–6. 
  25. ^ Thornton, Marion. Classical dynamics of particles and systems 5th. Brooks/Cole. 2004: pp. 53. ISBN 0534408966. 
  26. ^ Peter Graneau & Neal Graneau. In the Grip of the Distant Universe. : 147. 
  27. ^ Serway, Raymond, Principles of physics: a calculus-based text, Cengage Learning: pp. 99, 2006, ISBN 9780534491437 
  28. ^ 28.0 28.1 Misner, Charles; Thorne, Kip; John, Wheeler, Gravitation illustrated, Macmillan: pp. 543–549, 1973, ISBN 9780716703440 

外部链接

[编辑]


检索自“https://wikicn.playgoteam.workers.dev/w/index.php?title=慣性&oldid=83634983”