摺紙公理 ,又稱藤田-羽鳥公理 或藤田-賈斯汀公理 ,是摺紙數學 的基本公理。假定所有摺紙操作均在理想的平面 上進行,並且所有摺痕都是直線,那麼這些公理描述了通過摺紙可能達成的所有數學操作。
摺紙定理最早於1989年由雅克·賈斯汀(Jacques Justin)發現[ 1] 日 裔意大利 數學家藤田文章 發現[ 2]
前6個公理又叫做藤田公理,公理7由羽鳥公士郎發現,賈斯汀和羅伯特·朗(Robert J. Lang)也同樣發現了公理7。7條公理如下:
給定兩點
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
有且僅有 一條摺痕同時過這兩點。
給定兩點
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
給定兩直線
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
給定一點
p
1
{\displaystyle p_{1}}
l
1
{\displaystyle l_{1}}
p
1
{\displaystyle p_{1}}
l
1
{\displaystyle l_{1}}
給定兩點
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
l
1
{\displaystyle l_{1}}
p
2
{\displaystyle p_{2}}
p
1
{\displaystyle p_{1}}
l
1
{\displaystyle l_{1}}
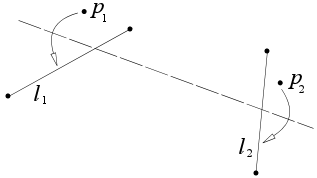
給定兩點
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
給定一點
p
{\displaystyle p}
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
l
2
{\displaystyle l_{2}}
p
1
{\displaystyle p_{1}}
l
1
{\displaystyle l_{1}}
公理5可能有最多2個解,公理6可能有最多3個解,而尺規作圖 的公理最多只有兩個解。所以,摺紙的作圖能力要強於尺規作圖。就是說,尺規作圖相當於在解二次方程,而摺紙幾何相當於解三次方程。因而諸如三等分角 、倍立方 等尺規作圖無法解決的問題卻可以用摺紙幾何解決。但是公理6在實踐中需要將紙「滑動」,這其實相當於二刻尺作圖 ,這在標準的尺規作圖中是不被允許的。
羅伯特·朗證明了這七個公理已經是摺紙幾何的全部公理了。
給定兩點
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
有且僅有 一條摺痕同時過這兩點。
以參數方程表示的話,過2點的直線可以表示為:
F
(
s
)
=
p
1
+
s
(
p
2
−
p
1
)
.
{\displaystyle F(s)=p_{1}+s(p_{2}-p_{1}).}
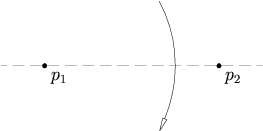
給定兩點
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
這條公理相當於是作線段
p
1
p
2
¯
{\displaystyle {\overline {p_{1}p_{2}}}}
垂直平分線 。這可以通過以下四個步驟完成:
使用公理1 作出連結
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
P
(
s
)
=
p
1
+
s
(
p
2
−
p
1
)
{\displaystyle P(s)=p_{1}+s(p_{2}-p_{1})}
找到直線
P
(
s
)
{\displaystyle P(s)}
中點
p
m
i
d
{\displaystyle p_{mid}}
找到垂直於
P
(
s
)
{\displaystyle P(s)}
向量
v
p
e
r
p
{\displaystyle \mathbf {v_{perp}} }
摺痕的參數方程 表示為:
F
(
s
)
=
p
m
i
d
+
s
⋅
v
p
e
r
p
.
{\displaystyle F(s)=p_{\mathrm {mid} }+s\cdot \mathbf {v} _{\mathrm {perp} }.}
給定兩直線
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
這條公理相當於是找出
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
l
1
{\displaystyle l_{1}}
q
1
{\displaystyle q_{1}}
q
2
{\displaystyle q_{2}}
l
2
{\displaystyle l_{2}}
u
{\displaystyle \mathbf {u} }
v
{\displaystyle \mathbf {v} }
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
u
=
(
p
2
−
p
1
)
/
|
(
p
2
−
p
1
)
|
{\displaystyle \mathbf {u} =(p_{2}-p_{1})/\left|(p_{2}-p_{1})\right|}
v
=
(
q
2
−
q
1
)
/
|
(
q
2
−
q
1
)
|
.
{\displaystyle \mathbf {v} =(q_{2}-q_{1})/\left|(q_{2}-q_{1})\right|.}
如果兩直線不平行,它們的交點為:
p
i
n
t
=
p
1
+
s
i
n
t
⋅
u
{\displaystyle p_{\mathrm {int} }=p_{1}+s_{\mathrm {int} }\cdot \mathbf {u} }
其中
s
i
n
t
=
−
v
⊥
⋅
(
p
1
−
q
1
)
v
⊥
⋅
u
.
{\displaystyle s_{int}=-{\frac {\mathbf {v} _{\perp }\cdot (p_{1}-q_{1})}{\mathbf {v} _{\perp }\cdot \mathbf {u} }}.}
兩條直線所夾的一個角的平分線方向是:
w
=
|
u
|
v
+
|
v
|
u
|
u
|
+
|
v
|
.
{\displaystyle \mathbf {w} ={\frac {\left|\mathbf {u} \right|\mathbf {v} +\left|\mathbf {v} \right|\mathbf {u} }{\left|\mathbf {u} \right|+\left|\mathbf {v} \right|}}.}
摺痕的參數方程是:
F
(
s
)
=
p
i
n
t
+
s
⋅
w
.
{\displaystyle F(s)=p_{\mathrm {int} }+s\cdot \mathbf {w} .}
這兩直線還有另一個角平分線,兩條角平分線互相垂直,且都過點
p
i
n
t
{\displaystyle p_{int}}
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
如果兩條直線平行 ,那麼只要沿着兩直線中間的一條線(與兩直線平行,到兩直線距離相等)摺疊就可以將
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
給定一點
p
1
{\displaystyle p_{1}}
l
1
{\displaystyle l_{1}}
p
1
{\displaystyle p_{1}}
l
1
{\displaystyle l_{1}}
向量
v
{\displaystyle \mathbf {v} }
l
1
{\displaystyle l_{1}}
F
(
s
)
=
p
1
+
s
⋅
v
.
{\displaystyle F(s)=p_{1}+s\cdot \mathbf {v} .}
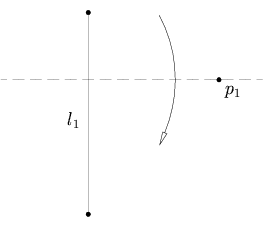
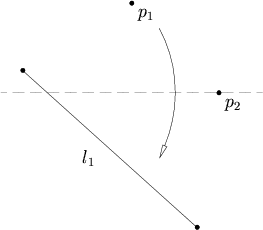
給定兩點
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
l
1
{\displaystyle l_{1}}
p
2
{\displaystyle p_{2}}
p
1
{\displaystyle p_{1}}
l
1
{\displaystyle l_{1}}
這個公理相當於找出圓 和直線的交點,所以有最多2個解,最少也可能無解。這取決於直線
l
1
{\displaystyle l_{1}}
p
2
{\displaystyle p_{2}}
p
2
{\displaystyle p_{2}}
p
1
{\displaystyle p_{1}}
如果我們知道直線上兩點
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})}
(
x
2
,
y
2
)
{\displaystyle (x_{2},y_{2})}
x
=
x
1
+
s
(
x
2
−
x
1
)
{\displaystyle x=x_{1}+s(x_{2}-x_{1})\,}
y
=
y
1
+
s
(
y
2
−
y
1
)
.
{\displaystyle y=y_{1}+s(y_{2}-y_{1}).\,}
如果圓心
p
2
=
(
x
c
,
y
c
)
{\displaystyle p_{2}=(x_{c},y_{c})}
r
=
|
p
1
−
p
2
|
{\displaystyle r=\left|p_{1}-p_{2}\right|}
(
x
−
x
c
)
2
+
(
y
−
y
c
)
2
=
r
2
.
{\displaystyle (x-x_{c})^{2}+(y-y_{c})^{2}=r^{2}.\,}
為了確定圓和直線的交點,將直線方程代入圓方程,得:
(
x
1
+
s
(
x
2
−
x
1
)
−
x
c
)
2
+
(
y
1
+
s
(
y
2
−
y
1
)
−
y
c
)
2
=
r
2
.
{\displaystyle (x_{1}+s(x_{2}-x_{1})-x_{c})^{2}+(y_{1}+s(y_{2}-y_{1})-y_{c})^{2}=r^{2}.\,}
或者可以簡化為:
a
s
2
+
b
s
+
c
=
0
{\displaystyle as^{2}+bs+c=0\,}
其中:
a
=
(
x
2
−
x
1
)
2
+
(
y
2
−
y
1
)
2
{\displaystyle a=(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}\,}
b
=
2
(
x
2
−
x
1
)
(
x
1
−
x
c
)
+
2
(
y
2
−
y
1
)
(
y
1
−
y
c
)
{\displaystyle b=2(x_{2}-x_{1})(x_{1}-x_{c})+2(y_{2}-y_{1})(y_{1}-y_{c})\,}
c
=
x
c
2
+
y
c
2
+
x
1
2
+
y
1
2
−
2
(
x
c
x
1
+
y
c
y
1
)
−
r
2
.
{\displaystyle c=x_{c}^{2}+y_{c}^{2}+x_{1}^{2}+y_{1}^{2}-2(x_{c}x_{1}+y_{c}y_{1})-r^{2}.\,}
然後,只要解以下方程就能確定直線和圓的交點:
−
b
±
b
2
−
4
a
c
2
a
.
{\displaystyle {\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.}
如果判別式
b
2
−
4
a
c
<
0
{\displaystyle b^{2}-4ac<0}
相切 ;如果辨別式大於0,方程有兩解,圓和直線有兩個交點。令
d
1
{\displaystyle d_{1}}
d
2
{\displaystyle d_{2}}
m
1
=
p
1
d
1
¯
{\displaystyle m_{1}={\overline {p_{1}d_{1}}}\,}
m
2
=
p
1
d
2
¯
.
{\displaystyle m_{2}={\overline {p_{1}d_{2}}}.\,}
摺痕
F
1
(
s
)
{\displaystyle F_{1}(s)}
m
1
{\displaystyle m_{1}}
p
1
{\displaystyle p_{1}}
d
1
{\displaystyle d_{1}}
F
2
(
s
)
{\displaystyle F_{2}(s)}
m
2
{\displaystyle m_{2}}
p
1
{\displaystyle p_{1}}
d
2
{\displaystyle d_{2}}
F
1
(
s
)
=
p
1
+
1
2
(
d
1
−
p
1
)
+
s
(
d
1
−
p
1
)
⊥
F
2
(
s
)
=
p
1
+
1
2
(
d
2
−
p
1
)
+
s
(
d
2
−
p
1
)
⊥
.
{\displaystyle {\begin{aligned}F_{1}(s)&=p_{1}+{\frac {1}{2}}(d_{1}-p_{1})+s(d_{1}-p_{1})_{\perp }\\[8pt]F_{2}(s)&=p_{1}+{\frac {1}{2}}(d_{2}-p_{1})+s(d_{2}-p_{1})_{\perp }.\end{aligned}}}
給定兩點
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
這個公理相當於找到同時與兩條拋物線 相切的直線,等價於解一個三次方程。兩條拋物線的焦點分別是
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
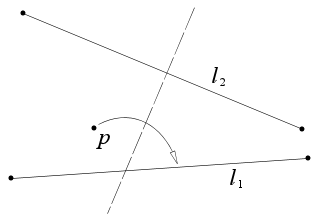
給定一點
p
{\displaystyle p}
l
1
{\displaystyle l_{1}}
l
2
{\displaystyle l_{2}}
l
2
{\displaystyle l_{2}}
p
1
{\displaystyle p_{1}}
l
1
{\displaystyle l_{1}}
過
p
{\displaystyle p}
l
2
{\displaystyle l_{2}}
l
1
{\displaystyle l_{1}}
q
{\displaystyle q}
p
q
¯
{\displaystyle {\overline {pq}}}
p
{\displaystyle p}
q
{\displaystyle q}
^ Justin, Jacques, "Resolution par le pliage de l'equation du troisieme degre et applications geometriques", reprinted in Proceedings of the First International Meeting of Origami Science and Technology , H. Huzita ed. (1989), pp. 251–261.
^ Humiaki Huzita, 「Understanding Geometry through Origami Axioms」, The
First International Conference on Origami in Education and Therapy (COET91) (1991)

















































![{\displaystyle {\begin{aligned}F_{1}(s)&=p_{1}+{\frac {1}{2}}(d_{1}-p_{1})+s(d_{1}-p_{1})_{\perp }\\[8pt]F_{2}(s)&=p_{1}+{\frac {1}{2}}(d_{2}-p_{1})+s(d_{2}-p_{1})_{\perp }.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7cf110005df528857c3e2c272bd402f014f14c1)