地圖投影列表
外觀
此處列出部分具有廣泛意義或有局部應用的地圖投影。由於地圖投影數量是無盡的[1],此列表並無終止。
投影
[編輯]註:嚴格而言,只要不滿足等角、等積的投影皆是折衷投影,但此處特意將等距投影列出。
| 投影名稱 | 示例地圖 | 類型 | 特性 | 發明者 | 年份 | 註釋 |
|---|---|---|---|---|---|---|
| 等距圓柱投影 | 
|
圓柱 | 等距 | 泰爾的馬里努斯 | 約120 | 幾何屬性最為簡單,沿經線的比例是準確的。需指定一條標準緯線。
Plate carrée:指定赤道為標準緯線時的特例。 |
| 卡西尼投影
(卡西尼-索德納投影) |
|
圓柱 | 等距 | 塞薩爾-弗朗索瓦·卡西尼·德·蒂里 | 1745 | 沿橫軸的等距圓柱投影。
沿中央經線的比例是準確的。 |
| 墨卡托投影 | 
|
圓柱 | 等角 | 傑拉杜斯·墨卡托 | 1569 | 同一方向的線為直線,利於航海。緯度越高畸變越大,不能顯示兩極。 |
| Web墨卡托投影 | 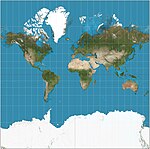
|
圓柱 | 折衷 | 2005 | 墨卡托投影的變形,使用球體代替橢球體以便於速算,且於南北緯約85.05°切斷,故投影后的地圖為正方形。此為互聯網上地圖服務的事實標準。 | |
| 高斯-克呂格投影 | 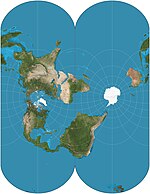
|
圓柱 | 等角 | 卡爾·弗里德里希·高斯、約翰·海因里希·路易斯·克呂格 | 1822 | 此投影與墨卡托不同,是橫軸橢球投影,有界。 |
| 魯西爾斜軸極平面投影 | 昂利·魯西爾
(Henri Roussilhe) |
1922 | ||||
| 洪特尼斜軸墨卡托投影 | 
|
圓柱 | 等角 | M·羅森蒙德(M. Rosenmund)、J·拉博德(J. Laborde)、馬丁·洪特尼(Martin Hotine) | 1903 | |
| 高爾極平面投影 | 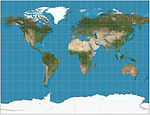
|
圓柱 | 折衷 | 詹姆斯·高爾 | 1855 | 試圖模仿墨卡托投影,但能顯示兩極。標準緯線為南北緯45°。 |
| 米勒圓柱投影 | 
|
圓柱 | 折衷 | 奧斯本·梅特蘭·米勒 | 1942 | 試圖模仿墨卡托投影,但能顯示兩極。 |
| 朗伯等積圓柱投影 | 圓柱 | 等積 | 約翰·海因里希·朗伯 | 1772 | 標準緯線是赤道。橫縱比是圓周率π。等積圓柱投影家族的基礎投影。 | |
| 伯爾曼投影 | 
|
圓柱 | 等積 | 沃爾特·伯爾曼 | 1910 | 蘭伯特等積投影的橫向壓縮版本。標準緯線為南北緯30°,長寬比約2.36。 |
| 霍波-戴爾投影 | 
|
圓柱 | 等積 | 米克·戴爾
(Mick Dyer) |
2002 | 蘭伯特等積投影的橫向壓縮版本。標準緯線約在南北緯37°,長寬比約2.0。 |
| 高爾-彼得斯投影 | 
|
圓柱 | 等積 | 詹姆斯·高爾(James Gall)、阿諾·彼得斯(Arno Peters) | 1855 | 蘭伯特等積投影的橫向壓縮版本。標準緯線約在南北緯45°,長寬比約1.6。 |
| 中心圓柱投影 | 
|
圓柱 | 透視 | 未知 | 約1850 | 由於極地變形過大,僅在全景攝影中使用。 |
| 正弦曲線投影
(桑遜-弗蘭斯蒂德投影) |
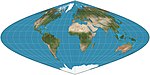
|
偽圓柱 | 等積、等距 | (發明者眾多,不知誰為第一人) | 約1600 | 經線呈正弦曲線狀,緯線分佈均勻,長寬比為2。緯線上的比例是正確的。 |
| 摩爾維德投影 | 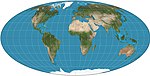
|
偽圓柱 | 等積 | 卡爾·摩爾維德 | 1805 | 經線呈橢圓弧形。 |
| 埃克特II型投影 | 
|
偽圓柱 | 等積 | 馬克斯·埃克特-格萊芬道夫(Max Eckert-Greifendorff) | 1906 | |
| 埃克特IV型投影 | 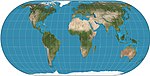
|
偽圓柱 | 等積 | 馬克斯·埃克特-格萊芬道夫 | 1906 | 緯線不等距且不等長;最外側的經線為半圓弧,其他為半橢圓弧。 |
| 埃克特VI型投影 | 
|
偽圓柱 | 等積 | 馬克斯·埃克特-格萊芬道夫 | 1906 | 緯線不等距且不等長;經線為半周期正弦曲線。 |
| 奧泰留斯橢圓投影 | 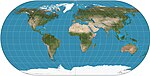
|
偽圓柱 | 折衷 | 巴蒂斯塔·阿格尼西(Battista Agnese) | 1540 |
經線是半圓弧。[2] |
| 古蒂等積投影 | 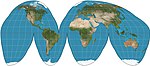
|
偽圓柱 | 等積 | 約翰·保羅·古蒂 | 1923 | 正弦曲線和摩爾維德投影的混合體,一般使用有裂縫的版本。 |
| 卡夫拉伊斯基VII型投影 | 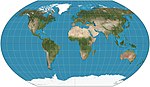
|
偽圓柱 | 折衷 | 弗拉基米爾·卡夫拉伊斯基 | 1939 | 緯線等距,在橫向上相當於壓縮至的瓦格納VI型投影。 |
| 羅賓森投影 | 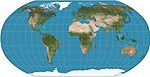
|
偽圓柱 | 折衷 | 亞瑟·H·羅賓森 | 1963 | Computed by interpolation of tabulated values. Used by Rand McNally since inception and used by NGS in 1988–1998. |
| 等積地球投影
(Equal Earth) |
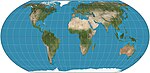
|
偽圓柱 | 等積 | Bojan Šavrič, Tom Patterson, Bernhard Jenny | 2018 | 受羅賓森投影的影響,但保持了等積特性。 |
| 自然地球投影
(Natural Earth) |
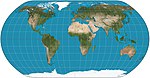
|
偽圓柱 | 折衷 | 湯姆·帕特森(Tom Patterson) | 2011 | 原本由表格插值製成,而今則由公式計算得來。 |
| 托布勒超橢圓投影 | 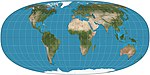
|
偽圓柱 | 等積 | 瓦爾多·R·托布勒 | 1973 | 一類地圖投影,摩爾維德投影、科利尼翁投影及一系列等積圓柱投影皆為其特例。 |
| 瓦格納VI型投影 | 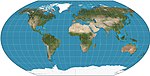
|
偽圓柱 | 折衷 | K. H. Wagner | 1932 | 相當於縱向上壓縮至的卡夫拉伊斯基VII型投影。 |
| 科利尼翁投影 | 偽圓柱 | 等積 | 愛德華·科利尼翁 | 約1865 | 此投影可將地球投影至一個菱形或兩個正方形上。 | |
| HEALPix | 
|
偽圓柱 | 等積 | 克齊斯多夫·果爾斯基(Krzysztof M. Górski) | 1997 | 科利尼翁投影和朗伯等積圓柱投影的混合體。 |
| Boggs eumorphic | 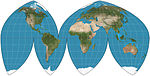
|
偽圓柱 | 等積 | 薩繆爾·魏特摩爾·博格斯(Samuel Whittemore Boggs) | 1929 | The equal-area projection that results from average of sinusoidal and Mollweide y-coordinates and thereby constraining the x coordinate. |
| 克拉斯特拋物線投影 | 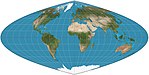
|
偽圓柱 | 等積 | 約翰·克拉斯特(John Craster) | 1929 | 經線呈拋物線,標準緯線為南北緯36°46′,緯線不均勻且比例不正確。長寬比2:1 。 |
| 麥克布萊德·托馬斯四次曲線投影 | 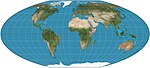
|
偽圓柱 | 等積 | 菲利克斯·W·麥克布萊德(Felix W. McBryde)、保羅·托馬斯(Paul Thomas) | 1949 | 標準緯線為南北緯33°45′,緯線不均勻且比例不正確,經線為四次曲線。僅中央經線與標準緯線交叉處比例是正確的。 |
| 四次等積投影 | 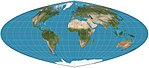
|
偽圓柱 | 等積 | 卡爾·齊蒙(Karl Siemon)、奧斯卡·亞當斯(Oscar Adams) | 1937、
1944 |
緯線不均勻且比例不正確,經線為四次曲線。赤道上無變形。 |
| 時報(泰晤士)投影 | 
|
偽圓柱 | 折衷 | 約翰·繆爾(John Muir) | 1965 | 標準緯線為南北緯45°。緯線基於高爾極平面投影,但經線是曲線。最初是為《時報(泰晤士)地圖冊》開發。 |
| 恆定方位角投影 | 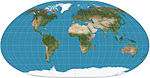
|
偽圓柱 | 折衷 | 卡爾·齊蒙(Karl Siemon)、Waldo R. Tobler | 1935
1966 |
從指定的中心點起的直線具有恆定方位角和正確的長度。一般不會沿赤道對稱。 |
| 艾托夫投影 | 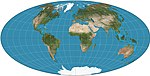
|
偽方位 | 折衷 | 大衛·A·艾托夫(David A. Aitoff) | 1889 | Stretching of modified equatorial azimuthal equidistant map. Boundary is 2:1 ellipse. Largely superseded by Hammer. |
| 漢默投影
(漢默-艾托夫投影) |
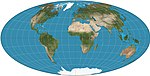
|
偽方位 | 等積 | 恩斯特·漢默(Ernst Hammer) | 1892 | Modified from azimuthal equal-area equatorial map. Boundary is 2:1 ellipse. Variants are oblique versions, centred on 45°N. |
| 斯特列伯投影 | 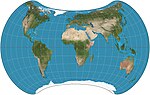
|
偽方位 | 等積 | Daniel "daan" Strebe | 1994 | Formulated by using other equal-area map projections as transformations. |
| 溫克爾三重投影 | 
|
偽方位 | 折衷 | 奧斯瓦爾德·溫克爾
(Oswald Winkel) |
1921 | 等距圓柱投影和艾托夫投影的算數平均。是美國國家地理學會1998年以來的標準世界地圖投影。 |
| 范德格林滕投影 | 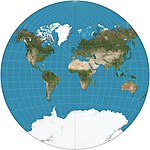
|
其他 | 折衷 | 阿爾馮斯·J·范德格林滕(Alphons J. van der Grinten) | 1904 | 邊界是圓形的。所有經緯線皆為圓弧。一般在南北緯80°截斷。是美國國家地理學會1922年至1988年間的標準世界地圖投影。 |
| 等距圓錐投影 | 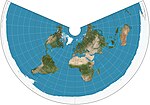
|
圓錐 | 等距 | 由托勒密第一投影得來 | 約100 | 經線比例正確,標準緯線的比例也正確。[3] |
| 朗伯等角圓錐投影 | 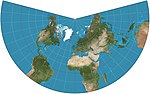
|
圓錐 | 等角 | 約翰·海因里希·朗伯 | 1772 | 航空地圖常用。 |
| 亞爾勃斯投影 | 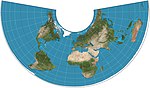
|
圓錐 | 等積 | 海因里希·亞爾勃斯 | 1805 | 兩條標準緯線,標準緯線之間變形很小。 |
| 維爾納投影 | 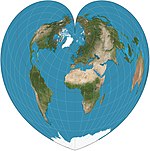
|
偽圓錐 | 等積、等距 | 約翰尼斯·斯塔比尤斯 | 約1500 | 緯線為間隔均勻的同心圓弧。從北極到地圖各處的距離皆是正確的。 |
| 彭納投影 | 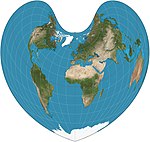
|
偽圓錐,心形 | 等積 | 伯納德斯·西爾瓦努斯(Bernardus Sylvanus) | 1511 | 緯線是間隔均勻的同心圓弧。整體形狀視參考緯線而異。是維爾納投影和正弦曲線投影的一般情況。 |
| 博通利投影 | 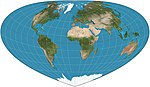
|
偽圓錐 | 等積 | 亨利·博通利
(Henry Bottomley) |
2003 | 可作為彭納投影的替代品,因其整體形狀較簡潔。緯線為橢圓弧。整體形狀視參考緯線而異。 |
| 美利堅多圓錐投影 | 
|
偽圓錐 | 折衷 | Ferdinand Rudolph Hassler | 約1820 | 緯線上的比例和中央經線的比例是正確的。 |
| 矩形多圓錐投影 | 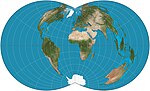
|
偽圓錐 | 折衷 | 美國國家大地測量局 | 約1853 | 可選擇不變形的緯線。經緯線互相垂直。 |
| 等差分緯線多圓錐投影 | 偽圓錐 | 折衷 | 中國地圖出版社 | 1963 | 多圓錐投影,緯線為圓弧且不共圓心。 | |
| 尼科洛西球形投影 | 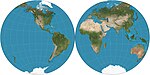
|
偽圓錐 | 折衷 | 比魯尼 | 約1000 | |
| 等距方位投影 | 
|
方位 | 等距 | 比魯尼 | 約1000 | 到中心的距離是正確的。聯合國會旗 即使用此投影,但在南緯60°切斷。 |
| 球心投影 | 
|
方位 | 球心透視 | 泰勒斯(可能) | 約580 BC | 大圓投影為直線,距離中心越遠,變形越大。只能顯示不到一個半球。 |
| 朗伯等積方位投影 | 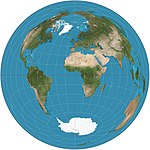
|
方位 | 等積 | 約翰·海因里希·朗伯 | 1772 | 從地圖中央到任意一點的距離都是沒有變形的。 |
| 球極平面投影 | 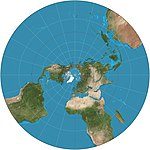
|
方位 | 等角 | 喜帕恰斯* | 約200 BC | 此投影沒有界,外側的半球變形嚴重,故通常會分為兩半球。由於圓形依然被投影為圓形,故可用於製作帶有隕石坑的全球地圖。 |
| 正投影 | 
|
方位 | 透視 | 喜帕恰斯* | 約200 BC | 相當於從無限遠處觀察。 |
| 垂直透視投影 | 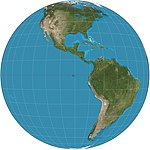
|
方位 | 透視 | 馬蒂亞斯·佐伊特(Matthias Seutter) | 1740 | 相當於從有限遠處觀察,故只能顯示少於一個半球。 |
| 雙點等距投影 | 
|
方位 | 等距 | 漢斯·毛勒
(Hans Maurer) |
1919 | 兩個「控制點」幾乎能任意選擇,且從該兩點中任一點到地圖上任意位置的距離都是不變形的。 |
| Gott, Goldberg and Vanderbei’s | 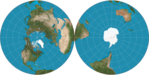 |
Azimuthal | Equidistant | J. Richard Gott, Goldberg and Robert J. Vanderbei | 2021 | 儘量縮小各種變形,並可印刷在一張光盤的兩面。[4][5][6] |
| 皮爾士梅花投影 | 
|
其他 | 等角 | 查爾斯·桑德斯·皮爾士 | 1879 | 可拼貼。除了四個奇點外的所有縫隙都是密合的。 |
| 居由氏投影 | 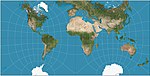
|
其他 | 等角 | Émile Guyou | 1887 | 橫縱比2:1。可拼貼。 |
| 亞當斯氏正方形半球投影 | 
|
其他 | 等角 | Oscar Sherman Adams | 1925 | |
| 李氏四面體投影 | 
|
多面體 | 等角 | L. P. Lee | 1965 | 把地球投影在四面體上。可拼貼。 |
| 卦限投影 | 
|
多面體 | 折衷 | 列奧納多·達·文西 | 1514 | 將地球分為八個卦限,每個卦限為一個勒洛三角形。 |
| 凱西爾蝴蝶投影 | 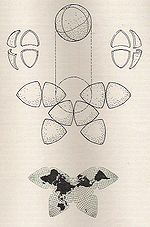
|
多面體 | 折衷 | 伯納德·約瑟夫·斯坦尼斯勞斯·凱西爾 | 1909 | 將地球投影為八面體,使得陸地之間是連續的。 |
| 凱西爾-凱耶斯投影 | 
|
多面體 | 折衷 | 吉恩·凱耶斯 | 1975 | 將地球投影為截角八面體,使得陸地之間是連續的。 |
| 沃特曼蝴蝶投影 | 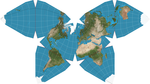
|
多面體 | 折衷 | Steve Waterman | 1996 | 將地球投影為截角八面體,使得陸地之間是連續的。 |
| Quadrilateralized spherical cube | 多面體 | 等積 | F. Kenneth Chan, E. M. O'Neill | 1973 | ||
| Dymaxion map | 
|
多面體 | 折衷 | 巴克敏斯特·富勒 | 1943 | 又叫富勒投影。 |
| Authagraph | 
|
多面體 | 折衷 | 鳴川肇 | 1999 | 幾乎等積,可做成拼貼。 |
| 高多面體投影 | 多面體 | 等積 | 雅爾克·凡·魏克 | 2008 | 將地球投影為面數極高的多面體。[7][8] | |
| 克雷格反方位投影 (麥加投影) |
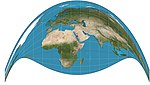
|
反方位 | 折衷 | 詹姆斯·愛爾蘭·克雷格
(James Ireland Craig) |
1909 | |
| 漢默反方位投影(正半球) | 
|
反方位 | Ernst Hammer | 1910 | ||
| 漢默反方位投影(背半球) | 
|
反方位 | Ernst Hammer | 1910 | ||
| 利特羅投影 | 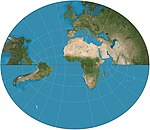
|
反方位 | 等角 | Joseph Johann Littrow | 1833 | on equatorial aspect it shows a hemisphere except for poles. |
| 犰狳投影 | 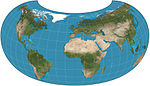
|
其他 | 折衷 | Erwin Raisz | 1943 | |
| GS50投影 | 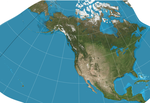
|
其他 | 等角 | 約翰·P·斯奈德 | 1982 | 用於顯示美國50個州,且儘量減小變形。 |
| 瓦格納VII型投影 | 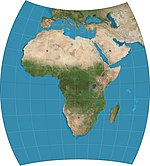
|
偽方位 | 等積 | K·H·瓦格納
(K. H. Wagner) |
1941 | |
| 橫軸摩爾維德投影 | 
|
偽圓柱 | 等積 | 約翰·巴托洛繆(John Bartholomew) | 1948 | 摩爾維德投影的傾斜版。 |
| 貝爾當投影 | 
|
其他 | 折衷 | 雅克·貝爾當(Jacques Bertin) | 1953 | 修改變形方式,增大海洋變形並減小陸地變形。通常用於法國的地緣政治地圖。[9] |
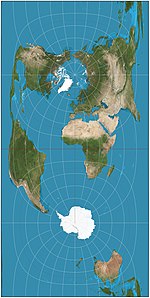
| 廣義等差分緯線多圓錐投影 | 
|
偽圓錐 | 折衷 | 郝曉光[10] | 2001 | 等差分緯線多圓錐投影的坐標變換版本;用於中國人民解放軍的官方軍事地圖,亦用於國家海洋局的極地探險用途。[11][12] |
參考文獻
[編輯]- ^ Snyder, John P. Flattening the earth: two thousand years of map projections. University of Chicago Press. 1993: 1. ISBN 0-226-76746-9.
- ^ Donald Fenna. Cartographic Science: A Compendium of Map Projections, with Derivations. CRC Press. 2006: 249. ISBN 978-0-8493-8169-0.
- ^ Furuti, Carlos A. Conic Projections: Equidistant Conic Projections. [February 11, 2020]. (原始內容存檔於November 30, 2012).
- ^ New Earth Map Projection. vanderbei.princeton.edu. [2023-04-27]. (原始內容存檔於2023-04-27).
- ^ Fuller-Wright, Liz. Princeton astrophysicists re-imagine world map, designing a less distorted, 'radically different' way to see the world. Princeton University. [2022-07-13]. (原始內容存檔於2022-07-13) (英語).
- ^ Gott III, J. Richard; Goldberg, David M.; Vanderbei, Robert J. Flat Maps that improve on the Winkel Tripel. 2021-02-15. arXiv:2102.08176
 [astro-ph.IM].
[astro-ph.IM].
- ^ Jarke J. van Wijk. Unfolding the Earth: Myriahedral Projections. [2023-11-30]. (原始內容存檔於2020-06-20).
- ^ Carlos A. Furuti. Interrupted Maps: Myriahedral Maps. [2023-11-30]. (原始內容存檔於2020-01-17).
- ^ Rivière, Philippe. Bertin Projection (1953). visionscarto. October 1, 2017 [January 27, 2020]. (原始內容存檔於2020-01-27).
- ^ 郝曉光; 薛懷平. 纬线世界地图 (PDF) (1): 第95–99頁. 2001年2月 [2024-05-10]. (原始內容存檔 (PDF)於2022-07-05).
- ^ Alexeeva, Olga; Lasserre, Frédéric. Le concept de troisième pôle: cartes et représentations polaires de la Chine. Géoconfluences. October 20, 2022 [February 14, 2023]. (原始內容存檔於February 14, 2023) (French).
- ^ Vriesema, Jochem. Arctic geopolitics: China’s remapping of the world. Clingendael Spectator. The Hague: Clingendael. April 7, 2021 [February 14, 2023]. (原始內容存檔於February 14, 2023).

