卡西尼定律
外觀
卡西尼定律(Cassini's laws)對月球的運動提供了一種簡潔的敘述。本定律是由著名科學家喬瓦尼·多梅尼科·卡西尼在1693年提出的[1]。
這之後科學界對卡西尼定律的改進包括天平動機制的改進[1],並且已經擴大應用到其它的行星和衛星[2][3][4]。
卡西尼的定律
[編輯]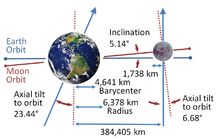
- 月球有着1:1 轉動-軌道共振。這意味着月球的自轉/軌道比率使得月球永遠以同一面朝向地球。
- 月球的自轉軸對黃道面保持固定的傾斜角度。月球的自轉軸形成的角錐與黃道面相交成圓形。
- 包含黃道面的法線和月球軌道平面的法線形成的平面會包含月球的自轉軸。
在月球的狀況,他的自轉軸總是指向離開北黃極1.5度,軌道平面的法線和自轉軸永遠在黃道平面法線的兩側相對着。
因此,軌道平面的法線和月球自轉軸的進動,兩者以相同的週期繞着黃極運動,這個週期大約是18.6年,並且運動的方向是逆行的。
卡西尼狀態
[編輯]一個遵守這些定律的系統被稱為「卡西尼狀態」(Cassini state),那就是:一種進化的轉動狀態,當軌道傾角固定不變時,自轉軸、軌道的法線、和拉普拉斯平面的法線是共平面的[2][3][5]。拉普拉斯平面是被定義為行星的軌道進動與赤道和黃道有着固定傾角的平面[5]。
卡西尼狀態1的定義是自轉軸和軌道面垂直軸和拉普拉絲平面的垂直軸在同一側。卡西尼狀態2則是自轉軸和軌道面垂直軸和拉普拉斯平面的垂直軸在相對側。[6]。地球的月球為卡西尼狀態2。
參考資料與註釋
[編輯]- ^ 1.0 1.1 卡西尼定律的原始敘述請見V V Belet︠s︡kiĭ. Essays on the Motion of Celestial Bodies. Birkhäuser. 2001: 181. ISBN 3-7643-5866-1.
- ^ 2.0 2.1 Peale, Stanton J. Generalized Cassini's Laws. The Astronomical Journal. 1969, 74: 483. Bibcode:1969AJ.....74..483P. ISSN 0004-6256. doi:10.1086/110825.
- ^ 3.0 3.1 Yseboodt, Marie; Margot, Jean-Luc. Evolution of Mercury's obliquity (PDF). Icarus. 2006, 181 (2): 327–337 [2019-03-14]. Bibcode:2006Icar..181..327Y. ISSN 0019-1035. doi:10.1016/j.icarus.2005.11.024. (原始內容存檔 (PDF)於2018-10-01).
- ^ V V Belet︠s︡kiĭ. Essays on the Motion of Celestial Bodies. Birkhäuser. 2001: 179. ISBN 3-7643-5866-1.
- ^ 5.0 5.1 Y. Calisesi. Solar Variability and Planetary Climates. Springer. 2007: 34. ISBN 0-387-48339-X.
- ^ J. N. Winn and M. J. Holman (2005),"Obliquity Tides on Hot Jupiters", The Astrophysical Journal, Volume 628, Issue 2, pp. L159-L162.
延伸閱讀
[編輯]- Cassini Laws – from Eric Weisstein's World of Physics (頁面存檔備份,存於互聯網檔案館)
- Eckhardt, Donald H. Theory of the Libration of the Moon. Earth, Moon, and Planets (Springer Netherlands). 1981, 25: 3–49. Bibcode:1981M&P....25....3E. doi:10.1007/BF00911807.
- Cassini's 3 laws (頁面存檔備份,存於互聯網檔案館)
- Cassini's laws (頁面存檔備份,存於互聯網檔案館)
