六面體
| 部分的六面體 | |
|---|---|
 三方偏方面體 |
 五角錐 |
 四角柱 |
 雙三角錐 |
在幾何學中,六面體是指由六個面組成的多面體。所有面都全等、所有邊等長且所有角相等的六面體稱為正六面體。幾何學上的正六面體是立方體,由6個正方形組成,但在抽象幾何學中有另外一種具有6個面的正多面體,是由6個正五邊形組成的半十二面體,但其為抽象多胞形不具有體積。其他亦存在所有面都全等但其他條件未必符合正多面體的形狀,例如雙三角錐和菱形六面體。其他也存在許多不規則的六面體,例如四角錐台、五角錐等。
常見的六面體
[編輯]常見的六面體有正方體、四角柱、五角錐、雙三角錐、三方偏方面體。
長方體
[編輯]六個面都是矩形的六面體稱為長方體,長方體具有每個二面角相等和每個三面角相等等特性。
平行六面體
[編輯]六個面都是平行四邊形的六面體稱為平行六面體。當六個面都是菱形時,則具有等邊多面體的性質,此時稱為菱形六面體。
六面體列表
[編輯]| 名稱 | 圖像 | 頂點 | 邊 | 面 | 面的種類 | 對稱性 | 展開圖 |
|---|---|---|---|---|---|---|---|
| 立方體 (正多面體) |

|
8 | 12 | 6 | 6個正方形 |
Oh, [4,3], (*432) order 48 |

|
| 長方體 | 
|
8 | 12 | 6 | 6個矩形 |
D2h, [2,2], (*222) order 8 |

|
| 四角柱 (柱體群) |

|
8 | 12 | 6 | 2個四邊形 4個矩形 |
D4h, [4,2], (*422), order 16 | |
| 五角錐 (錐體群) |

|
6 | 10 | 6 | 1個五邊形 5個三角形 |
C5v, [5], (*55) | 
|
| 四角錐台 | 
|
8 | 12 | 6 | 2個四邊形 4個梯形 |
C4v, [4], (*44) order 8 | |
| 菱形六面體 | 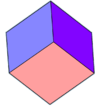
|
8 | 12 | 6 | 6個菱形 |
D3d, [2+,6], (2*3) order 12 | |
| 三方偏方面體 | 
|
8 | 12 | 6 | 6個四邊形 |
D3, [2,3]+, (223) order 6 | |
| 雙三角錐 | 
|
5 | 9 | 6 | 6個三角形 |
D3h, [3,2], (*223) order 12 | 
|
| 平行六面體 | 
|
8 | 12 | 6 | 6個平行四邊形 |
Ci, [2+,2+], (×) order 2 | |
| 平行六面體 (由菱形組成) |

| ||||||
| 十二面體半形 | 
|
10 | 15 | 6 | 6個五邊形 |
A5, order 60 | |
| 皮特里正十二面體 | 
|
20 | 30 | 6 | 6個扭歪十邊形 |
A5×C2, with 120 elements | |
| 皮特里正二十面體 | 
|
12 | 30 | 6 | 6個扭歪十邊形 |
||
| 六面形 | 
|
2 | 6 | 6 | 6個二角形 |
D6h(*666) | |
| 二角反稜柱 | 
|
4 | 8 | 6 | 2個二角形 4個三角形 |
D2d, [2+,4], (2*2), order 8 |
非凸六面體
[編輯]| 非凸六面體 | ||
|---|---|---|
 面的種類:4.4.3.3.3.3 10條邊、 6個頂點 |
 面的種類:5.5.3.3.3.3 11條邊、 7個頂點 |
 面的種類:6.6.3.3.3.3 12條邊、 8個頂點 |
退化六面體
[編輯]部份六面體包含退化的面或者本身已經退化至無法擁有體積的形式。例如二角反稜柱,其2個底面為二角形,因此退化成一條稜、更進一步的退化六面體有六面形,其由6個二角形組成,本身已退化至無法擁有體積的形式,僅能以球面鑲嵌的形式存在。
二角反稜柱
[編輯]二角反稜柱,又稱反二角柱是指底面為二角形的反稜柱,由於其兩個底面皆為二角形,因此這兩個面已退化成一條稜,若不計這兩個退化的底面,則這個立體與四面體無異。在球面幾何學中,二角反稜柱可以作為球面鑲嵌,此時二角形的面能夠在求面上已非退化的形式存在,而確保整個立體為六個面組成的立體,此時的二角反稜柱由2個球面二角形和4個球面三邊形構成,共有6個面、8條邊和4個頂點,並且可以視為扭稜的二面形或二角形二面體,在施萊夫利符號中可以用sr{2,2}來表示。
 二角反稜柱。上方及下方紅色的線段為退化的二角形底面。若不計這兩個退化底面,則整個立體與四面體無異 |
 作為球面鑲嵌的二角反稜柱。計入二面形面時,二角反稜柱是一種六面體 |
六面形
[編輯]
六面形是一種多面形,為退化的六面體,無法擁有體積,由六個二角形組成。在球面幾何學中,六面形可以在球面上以鑲嵌的方式存在,表示六個鑲嵌在球體上的球弓形,施萊夫利符號中利用{2,6}來表示,其對偶多面體是六邊形二面體。
六面形由六個二角形組成,每個頂點都是六個二角形的公共頂點。正六面形的每個面都是正二角形,且每個頂點都是六個正二角形的公共頂點,因此正六面形也可以視為一種正多面體,但是因為其已退化,因此不會與柏拉圖立體一同討論。
六面形具有D6h, [2,6], (*226)的對稱性和D6, [2,6]+的旋轉對稱性,且階數為24,在考克斯特符號中用![]()
![]()
![]()
![]()
![]() 表示,其對稱性與六角柱相同,因此六角柱也可以視為一種與六面形相關的立體,因為六角柱可以經由六面形透過截角變換構造。
表示,其對稱性與六角柱相同,因此六角柱也可以視為一種與六面形相關的立體,因為六角柱可以經由六面形透過截角變換構造。
拓樸學中的六面體
[編輯]在所有凸六面體當中,共有七種拓樸結構有明顯差異的凸六面體[1][2][3][4][5] 。其中有2中互為鏡射像。
 雙三角錐 36 9 E, 5 V |
 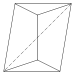 四角反楔體。 有一個手性鏡像 面的種類:4.4.3.3.3.3 10條邊, 6個頂點 |
 面的種類:4.4.4.4.3.3 11條邊, 7個頂點 |
 五角柱 面的種類:5.35 10條邊, 6個頂點 |
 面的種類:5.4.4.3.3.3 11條邊, 7個頂點 |
 面的種類:5.5.4.4.3.3 12條邊, 8個頂點 |
參考文獻
[編輯]- ^ Anatole Beck, Michael Bleicher, Donald Crowe. Excursions into Mathematics: 29–30. 1969.
- ^ Counting polyhedra (頁面存檔備份,存於互聯網檔案館) numericana.com [2016-1-10]
- ^ Martin Gardner. Denkspiele von anderen Planeten. München: Hugendubel. 1986: 134. ISBN 3-88034-295-4.
- ^ Weisstein, Eric W. (編). Hexahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英語).
- ^ Gardner, M. "Find the Hexahedrons." §19.9 in Martin Gardner's New Mathematical Diversions from Scientific American. New York: Simon and Schuster, pp. 224-225 and 233, 1966.
外部連結
[編輯]- Polyhedra with 4-7 Faces by Steven Dutch
