1 + 1 + 1 + 1 + …

級數1 + 1 + 1 + 1 + ⋯

平滑化之後

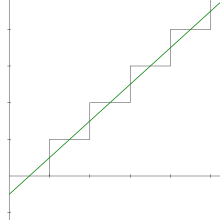
平滑化後的漸近特性，此直線在y軸的截軸為−1/2

1 + 1 + 1 + 1 + …，亦寫作 $\sum _{n=1}^{\infty }n^{0}$, $\sum _{n=1}^{\infty }1^{n}$或$\sum _{n=1}^{\infty }1$，是一個發散級數，表示其部份和形成的數列不會收斂。數列1ⁿ可以視為公比為1的等比級數。不同於其他公比為有理數的等比級數，此級數不但在實數下不收斂，在某些特定數字p的p進數下也不收斂。若在擴展的實數軸中，因為部份和形成的數列單調遞增且沒有上界，因此級數的值如下：

$\sum _{n=1}^{\infty }1=+\infty \,,$

此發散級數無法用切薩羅求和及阿貝爾和的求和法求和。

當出現於物理運用時，它也解釋為ζ函數正規化，它是黎曼ζ函數在零點的取值。

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{1-2^{1-s}}}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{s}}}\,,$

上述二個公式在$s=0$時不成立，必需利用解析連續定義。

$\zeta (s)=2^{s}\pi ^{s-1}\ \sin \left({\frac {\pi s}{2}}\right)\ \Gamma (1-s)\ \zeta (1-s)\!,$

用上式求得（假設$\Gamma (1)=1$）

$\zeta (0)={\frac {1}{\pi }}\lim _{s\rightarrow 0}\ \sin \left({\frac {\pi s}{2}}\right)\ \zeta (1-s)={\frac {1}{\pi }}\lim _{s\rightarrow 0}\ \left({\frac {\pi s}{2}}-{\frac {\pi ^{3}s^{3}}{48}}+...\right)\ \left(-{\frac {1}{s}}+...\right)=-{\frac {1}{2}}\!$

以下ζ(s)在s = 1時的級數展開：也是這種意義下此級數的和：

1 + 1 + 1 + 1 + · · · = ζ(0) = −¹⁄₂

也可用其他的s值來為其他的級數求和，例如ζ(-1)=1 + 2 + 3 + 4 + ⋯=–1/12，ζ(-2)=1 + 4 + 9 + ... = 0，其通式為

$\zeta (-s)=\sum _{n=1}^{\infty }n^{s}=1^{s}+2^{s}+3^{s}+\ldots =-{\frac {B_{s+1}}{s+1}}$

其中B_k為伯努利數。

在同一年內，有兩位傑出的物理學家斯拉夫諾夫（A. Slavnov）和F. Yndurain 分別在巴塞羅那作了學術演講。兩場學術演講的主題不同，但是在這兩個人的介紹當中，都說到了一句令觀眾非常難忘的話：「各位都知道，1 + 1 + 1 + 1 + … = −1⁄2」，某程度意味著「如果觀眾不知道這個，那麼繼續聽下去是沒有意義的。」