等边图形
在几何学中，等边或称边可递是指所有边都相等的几何图形，同时其对称性可以在其边上传递。通俗地说，这意味著这个几何结构中只有一种类型的边，同时在这个立体上任选两个边，并透过平移、旋转或镜射等变换将一边变换到另一个边的位置时，其仍占有相同的空间区域。
边可递多边形
[编辑]边可递多边形是偶数边数的等边多边形。并非所有等边多边形都是边可递多边形。边可递多边形的对偶多边形是等角多边形。[1]
通常边可递2n边形具有Dn (*nn)的二面体群对称性。[2]例如菱形是一种边可递多边形，并具备D2 (*22)的二面体群对称性。[2]所有正多边形都是边可递多边形[3]:48，并具有2倍的最小对称性阶数：正n边形具有Dn (*nn)的二面体群对称性。
边可递2n边形可以用符号{nα}来表示，其中α代表最外侧的内角。第二外侧的内角β可能大于或小于180度。星形多边形也可以是边可递多边形，其可以用符号{(n/q)α}来表示，其中q<n-1且n和q互质（gcd(n,q)=1），而q代表转数或密度[4]。
| 边数 （2n） | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
|---|---|---|---|---|---|---|---|
| {nα} 凸 β<180 凹 β>180 |
 {2α} |
  {3α} |
  {4α} |
  {5α} |
  {6α} |
  {7α} |
  {8α} |
| 2转 {(n/2)α} |
-- |  {(3/2)α} |
 2{2α} |
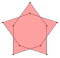  {(5/2)α} |
  2{3α} |
  {(7/2)α} |
  2{4α} |
| 3转 {(n/3)α} |
-- | -- |  {(4/3)α} |
 {(5/3)α} |
 3{2α} |
  {(7/3)α} |
  {(8/3)α} |
| 4转 {(n/4)α} |
-- | -- | -- |  {(5/4)α} |
 2{(3/2)α} |
 {(7/4)α} |
 4{2α} |
| 5转 {(n/5)α} |
-- | -- | -- | -- |  {(6/5)α} |
 {(7/5)α} |
 {(8/5)α} |
| 6转 {(n/6)α} |
-- | -- | -- | -- | -- |  {(7/6)α} |
 2{(4/3)α} |
| 7转 {(n/7)α} |
-- | -- | -- | -- | -- | -- |  {(8/7)α} |
边可递多面体与镶嵌
[编辑]所有正多面体都具备等面（面可递）、等边（边可递）和等角（点可递）的特性[5]。
拟正多面体或拟正镶嵌图，例如截半立方体和截半二十面体，其同时具备了等角（点可递）与等边（边可递）的特性，但不具备等面（面可递）的特性。[6][7]其对偶多面体，如菱形十二面体和菱形三十面体具备等面与等边的特性，而不具备等角的特性。
| 拟正 多面体 |
对偶拟正 多面体 |
拟正 星形多面体 |
对偶拟正 星形多面体 |
拟正 镶嵌图 |
对偶拟正 镶嵌图 |
|---|---|---|---|---|---|
 截半立方体具备等角与等边的特性 |
 菱形十二面体具备等面与等边的特性 |
 大截半二十面体为具备等角与等边特性的星形多面体 |
 大菱形三十面体为具备等面与等边特性的星形多面体 |
 截半六边形镶嵌为具备等角与等边特性的镶嵌图 |
 菱形镶嵌为具备等面与等边特性的镶嵌图 |
并非所有由正多边形组成的多面体或镶嵌都是边可递的，就算他所有边都等长，也可能因为边的相邻面不同（棱的组成不同）而导致其不满足边可递的特性。例如截角二十面体（足球的形状）就不满足边可递的特性，因为它具有两种类型的边：六边形-六边形公共边和六边形-五边形公共边，并且立体的对称性不允许将六边形-六边形边移动到六边形-五边形边。
边可递多面体所有棱的二面角皆相等。
凸多面体的对偶多面体仍为凸多面体[8]；非凸多面体的对偶多面体也仍为非凸多面体[8]；边可递多面体的对偶多面体亦仍为边可递多面体。
参见
[编辑]参考文献
[编辑]- ^ Guy, R.K. and Woodrow, R.E. The Lighter Side of Mathematics: Proceedings of the Eugene Strens Memorial Conference on Recreational Mathematics and Its History. Spectrum. Mathematical Association of America. 2020. ISBN 9781470457310.
- ^ 2.0 2.1 M Koca and N O Koca. Quasi Regular Polyhedra and Their Duals with Coxeter Symmetries Represented by Quaternions I. Journal of Physics: Conference Series (IOP Publishing). 2011-04, 284: 012039. doi:10.1088/1742-6596/284/1/012039.
- ^ Bisztriczky, T. and McMullen, P. and Schneider, R. and Weiss, A.I. Polytopes: Abstract, Convex and Computational. Nato Science Series C:. Springer Netherlands. 2012 [2022-07-10]. ISBN 9789401109246. （原始内容存档于2022-07-14）.
- ^ Grünbaum, Branko; Shephard, G. C. Tilings and Patterns
. W. H. Freeman. 1987. ISBN 978-0-7167-1193-3. 2.5 Tilings using star polygons, pp.82-85.
- ^ McLean, K. Robin, Dungeons, dragons, and dice, The Mathematical Gazette, 1990, 74 (469): 243–256, JSTOR 3619822.
- ^ Weisstein, Eric W. (编). Quasiregular Polyhedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
- ^ George W. Hart. Quasiregular polyhedra. [2022-07-11]. （原始内容存档于2013-05-24）.
- ^ 8.0 8.1 duality. maths.ac-noumea.nc. [2020-09-30]. （原始内容存档于2021-05-08）.
- Peter R. Cromwell. [[:多面體 (書籍)|Polyhedra]]. Cambridge University Press. 1997. ISBN 0-521-55432-2. 网址－维基内链冲突 (帮助) p. 371 Transitivity
