折线

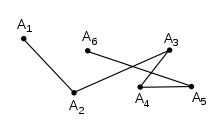

折线又称多边形链(polygonal chain)[注 1]或多段线(polyline)[5]是指一系列相连的线段,通常是一些任意不同方向的直线段首尾相连结所形成的线[7]。 与多边形不同,折线并不要求线的整体要头尾封闭。 更正式地说,折线P是由一系列称为其顶点的点所决定的曲线,该曲线连续地由线段连接这些顶点所构成。
变体
[编辑]简单折线
[编辑]简单折线是指该折线的线段连续相交,且仅有在线段的端点相交,没有在别处有相交(即非自相交的折线)。
封闭折线
[编辑]封闭折线是指第一个顶点与最后一个顶点重合,或者第一个顶点与最后一个顶点也相连的折线。[8] 平面的简单封闭折线是简单多边形的边界。 通常,“多边形”这个术语就是指“封闭折线”,但在某些情况下还是会将封闭折线和多边形两个概念区分开来。
单调折线
[编辑]如果存在一条直线L,且垂直于L的每条直线最多与该折线相交一次,则称该折线是一个单调折线。每个非平凡的单调多边形链都是非封闭的(开放的)。 相较之下,每个单调多边形(封闭折线)都恰好可以分割成两个单调折线。[9] 分段线性函数的图形相对于水平线形成单调折线。 一般的折线图也都是相对于某座标轴的单调折线。
参数化
[编辑]
折线的每个线段通常使用连续顶点间的线性插值来线性参数化。 在实际应用中,对于整条折线而言有两种常见的参数化方式。 一种是:折线之线段链的每一段都可以被分配与第一个顶点对应索引的参数之单位区间; 另一种是:折线之线段链的每一段都可以被分配一个与该段的长度相对应的参数区间,使得该参数沿著整个折线之线段链统一对应于其曲线长。
与点集的关联
[编辑]每个至少有n个点的点集都包含一条至少有条边的斜率正负相同之折线路径。 这是埃尔多斯-塞克雷斯定理的推论。
应用
[编辑]折线通常可以用来近似更复杂的曲线。 在这种情况下,道格拉斯-普克演算法可以用于寻找具有最少线段但又足够接近原始曲线的折线,作为该曲线精确的近似。[10][11]
在图绘制中,折线常用于表示图的边,在绘图样式中,将边绘制为直线段可能会导致交叉、边与顶点碰撞或其他不希望出现的特征。 在这种情况下,通常希望用尽可能少的线段和弯曲来绘制图的边,以减少绘图中的视觉混乱; 最小化弯曲次数的问题称为弯曲最小化问题。[12]
折线也是计算几何的一种基本资料类型。 例如,李德财和普雷帕拉塔的点定位演算法就是透过将任意曲面细分分解为单调折线的有序序列来进行操作,以达到可以透过二分搜寻来解决点位置查询问题的目标; 此方法后来经过改进,使得点定位问题的时间复杂度得到最佳化。[13]
参见
[编辑]注释
[编辑]参考文献
[编辑]- ^ Gomes, Jonas; Velho, Luiz; Costa Sousa, Mario, Computer Graphics: Theory and Practice, CRC Press: 186, 2012, ISBN 9781568815800.
- ^ Cheney, Ward, Analysis for Applied Mathematics, Graduate Texts in Mathematics 208, Springer: 13, 2001, ISBN 9780387952796.
- ^ 3.0 3.1 Boissonnat, Jean-Daniel; Teillaud, Monique, Effective Computational Geometry for Curves and Surfaces, Springer: 34, 2006, ISBN 9783540332596.
- ^ Muggeo, Vito M. R., segmented: An R package to fit regression models with broken-line relationships (PDF), R News, May 2008, 8 (1): 20–25
- ^ 5.0 5.1 折線 polyline. 双语词汇、学术名词暨辞书资讯网. 国家教育研究院. [2023-12-03]. (原始内容存档于2023-12-03).
- ^ Open Geospatial Consortium, Herring, John R. , 编, OpenGIS® Implementation Standard for Geographic information - Simple feature access - Part 1: Common architecture, 1.2.1, Open Geospatial Consortium, 2011-05-28 [2016-01-15], (原始内容存档于2017-01-29)
- ^ 折線. 教育部重编国语辞典. [2023-11-17]. (原始内容存档于2023-11-17).
- ^ Mehlhorn, Kurt; Näher, Stefan, LEDA: A Platform for Combinatorial and Geometric Computing, Cambridge University Press: 758, 1999, ISBN 9780521563291.
- ^ O'Rourke, Joseph, Computational Geometry in C, Cambridge Tracts in Theoretical Computer Science, Cambridge University Press: 45, 1998, ISBN 9780521649766.
- ^ Ramer, Urs, An iterative procedure for the polygonal approximation of plane curves, Computer Graphics and Image Processing, 1972, 1 (3): 244–256, doi:10.1016/S0146-664X(72)80017-0.
- ^ Douglas, David; Peucker, Thomas, Algorithms for the reduction of the number of points required to represent a digitized line or its caricature, The Canadian Cartographer, 1973, 10 (2): 112–122, doi:10.3138/FM57-6770-U75U-7727.
- ^ Tamassia, Roberto, On embedding a graph in the grid with the minimum number of bends, SIAM Journal on Computing, 1987, 16 (3): 421–444, doi:10.1137/0216030.
- ^ Edelsbrunner, Herbert; Guibas, Leonidas J.; Stolfi, Jorge, Optimal point location in a monotone subdivision, SIAM Journal on Computing, 1986, 15 (2): 317–340, doi:10.1137/0215023.


