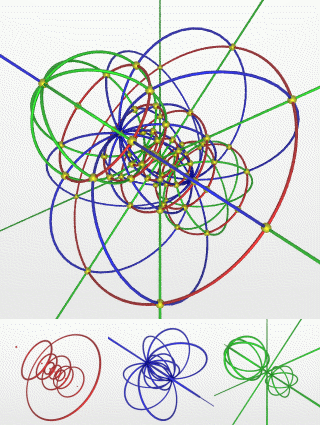
 超球面(hypersphere)的平行线(parallels)(红色)、 子午线(meridians)(蓝色)以及超子午线(hypermeridians)(绿色)的立体投影法(Stereographic projection)。 因为立体投影法的共形特性,这些曲线彼此在交点上彼此正交(图中黄色点),如同在四维空间中一样。所有曲线都是圆;交会在<0,0,0,1>的曲线具有无限大的半径(亦即:直线)。
超球面(hypersphere)的平行线(parallels)(红色)、 子午线(meridians)(蓝色)以及超子午线(hypermeridians)(绿色)的立体投影法(Stereographic projection)。 因为立体投影法的共形特性,这些曲线彼此在交点上彼此正交(图中黄色点),如同在四维空间中一样。所有曲线都是圆;交会在<0,0,0,1>的曲线具有无限大的半径(亦即:直线)。
数学中,三维球面(英文常写作3-sphere)是球面在高维空间中的类比客体。它由四维欧几里得空间中与一固定中心点等距离的所有点所组成。寻常的球面(或者说二维球面)是一个二维表面,而三维球面是一个具有三个维度的几何客体,这样的几何客体都可以归类为三维流形(3-manifold)。
三维球面也称作超球面(hypersphere),虽然这个辞汇可以更广义地代表任何n维球面,而n ≥ 3。
以座标表示,三维球面具有中心(C0, C1, C2, C3)及半径r 乃在R4符合条件

的所有点的集合:
(x0, x1, x2, x3)。
三维球面球心在原点,而半径是1的称为单位三维球面(unit 3-sphere),常写作S3:
 。
。
方便性上,常将R4另外以复数C2或四元数(quaternions)H等价表示。单位三维球面则可写为

或
 。
。
最后一个表示法常是最有用的。其将三维球面描述为所有单位四元数(绝对值为1的四元数)的集合。正如同所有单位复数的集合在复数几何是重要的,所有单位四元数的集合在四元数几何中也是重要的。
- 注意:此篇文章使用了n维空间的球面,称作n维球面(n-sphere)。





