殼層定理(Shell Theorem)是古典重力學上的理論,其可簡化重力於對稱球體內部和外部的貢獻,並且在天文學上有特別的應用。
殼層定理最先由牛頓在所推演出來[1],其闡明了
- 球對稱物體對於球體外的重力貢獻如同將球體質量集中於球心。
- 在對稱球體內部的物體不受其外部球殼的重力影響。
由殼層定理的結果亦可得知,在一質量均勻分布的球體,重力由表面至中心線性遞減至零。因為球殼不會對內部物體有重力之貢獻,而剩餘之質量(不包括球殼)是與r3成正比,而重力是正比於m/r2,因此重力與r3/r2 = r成正比。
在星體運動的分析中,殼層定理是非常重要的,因為其隱含地表示可將星體視為一個質點來計算。除了重力之外,殼層定理亦可描述均勻帶電球體所貢獻的電場,或者是其他平方反比定律的物理現象。
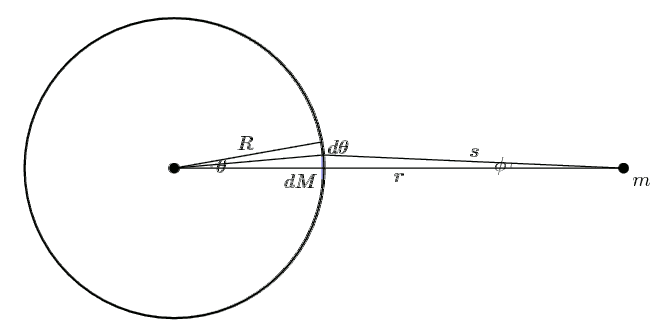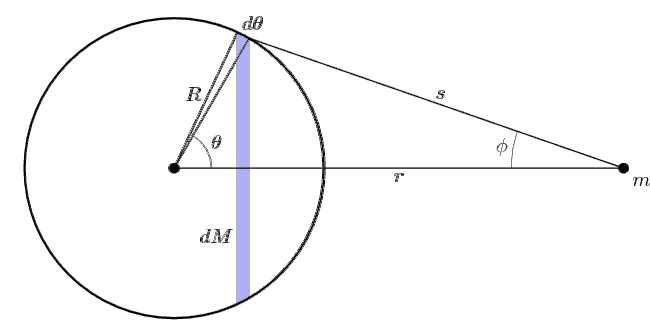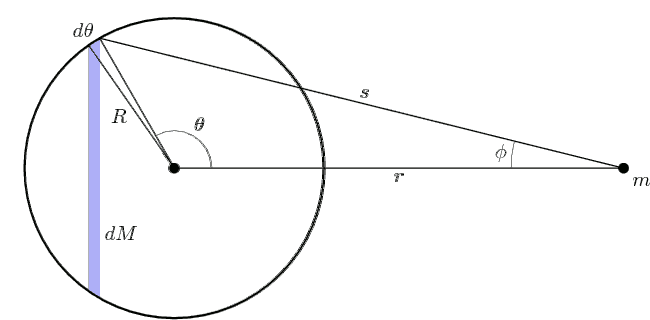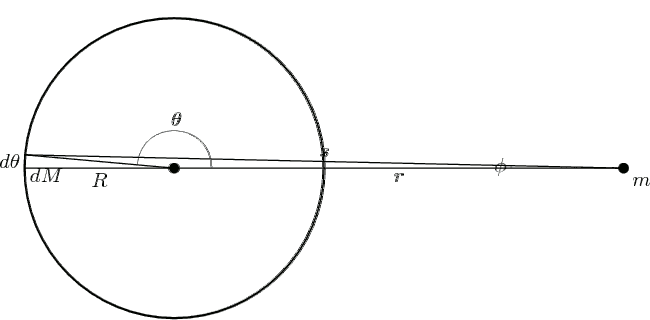
一個均勻實心的球體可視為由無限多個極薄的球殼所組成,而每個球殼均視為一個質點,所以先考慮以下灰色環狀區域:
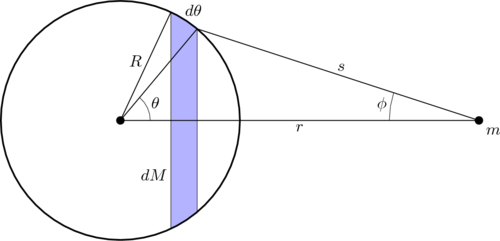 Shell-diag-1
Shell-diag-1
其中dθ是微分角度,非弧長。根據牛頓萬有引力定律,環狀區域對質點m的重力貢獻為[2]

力的方向指向球心。將所有的dFr積分,即為質點m之所受重力

接著,將dM表成與θ相關的函數。總球殼面積為

而灰色環狀區域的面積為

所以灰色環狀區域的質量dM可表為

因此

由餘弦定理可知


θ由0積分至π,φ由0增加到最大值再遞減至0,s由r - R變化至r + R。積分計算的過程如下圖所示。
 Shell-diag-1-anim
Shell-diag-1-anim
對前述之餘弦定理給出的關係式第二式做隱微分計算可得

因此Fr可變數變換為

所以

即薄球殼貢獻之重力如同將所有質量集中於球心。
接著,將每一個薄球殼dM累加起來,即是實心球體對外部物體的重力貢獻

其中 為所有薄球殼質量之總和,其實就是球體之質量,即
為所有薄球殼質量之總和,其實就是球體之質量,即

另外亦可以積分方式運算 如下:
如下:
在距球心x到x + dx的球殼質量dM可寫為

因此

即實心球對外部物體的重力貢獻如同將所有質量集中於球心。
球內重力情形可直接由球外重力Fr改變s之積分上下界推得,即自R - r積分至R + r,各參數的示意圖如下所示。
 Shell-diag-2
Shell-diag-2
所以薄球殼對內部物體的重力貢獻為

即球內物體不受外球殼(無論厚薄)的重力影響。
注意,這邊的計算係積分質點m外的球殼(即R > r),當R < r,即回到球體之外的重力情況。
若質點m在實心球內,只有半径小于r的那部分球体质量对质点m有净力作用,半径大于r的那部分球壳对m产生的重力场为0。小于 r 那部分球体的质量为

距离球心r处的重力场为

质点m受到这个实心球体产生的重力为

k是一个常数,  。
。
推廣:假設質點重力的形式為 ,那麼球殼內的重力為
,那麼球殼內的重力為

上式只有當 時,Fr才會等於0。
同樣地,在球殼外的重力為
時,Fr才會等於0。
同樣地,在球殼外的重力為

- ^ Newton, Isaac (1687). Philosophiae Naturalis Principia Mathematica. London. pp. Theorem XXXI.
- ^ Raymond A. Serway and John W. Jewett (2007), Physics for Scientists and Engineers with Modern Physics.




























