过冲

过冲示意图，伴有振铃和安定时间。

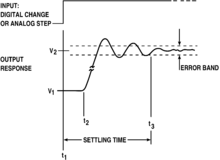
在信号处理、控制理论、电子学以及数学中，过冲（英語：overshoot），也称超调，是指信号或者函数超过了预期值，是暫態響應的特性之一。常见于类似低通滤波器的频带限制系统中阶跃响应阶段，通常会跟随有伴生的振铃。

定义

在尾形克彦的《离散时间控制系统》中，最大过冲量被定义为：“从系统期望响应值计算，响应曲线的最大峰值”。

控制理论

在控制理论中，过冲是指输出超过了它的最终稳态值。

对于阶跃输入，过冲率（percentage overshoot, PO）是指过冲最大值减去阶跃值再除以阶跃值。在单位阶跃中，过冲是最大阶跃响应值减一。

过冲率是基于阻尼系数 ζ 的函数：

$PO=100\%\cdot e^{\left({\frac {-\zeta \pi }{\sqrt {1-\zeta ^{2}}}}\right)}$

阻尼系数可表示为：

$\zeta ={\sqrt {\frac {(\ln PO)^{2}}{\pi ^{2}+(\ln PO)^{2}}}}$

电子学

电子信号中过冲与下冲。

在电子学中，过冲是指，从一个值转变到另一个值时，任何参数的瞬时值超过它的最终（稳态）值。过冲在放大器的输出信号中有重要的意义。

惯例: 过冲发生于瞬时值超过最终值。当瞬时值低于最终值时，也称为“下冲（undershoot）”。

一般电路设计，多半會使上升时间最小化，同時也將失真限制在可接受范围内。

1. 过冲表现为信号的失真。
2. 在电路设计中，最小化过冲与减小上升时间的目标会发生冲突。
3. 过冲的大小依赖于经历阻尼现象的时间。
4. 过冲通常伴有安定时间，即输出到达稳态的时长。

数学

正弦積分可以用來表示过冲

主条目：吉布斯现象

在函數近似時，过冲也是用來描述近似品質的一個特點。若一函數（例如方波）用許多函數的和（例如傅里叶级数或是正交多項式展開）來表示時，在原函數轉折的部份可能就會有过冲、下沖及振鈴的情形。若多項式的項次越多，近似函數和原函數的偏差也會減緩。不過近似項次越多，振盪週期會變長，但其振幅卻不會改變，這就是吉布斯现象。在傅里叶变换中，這可以用在一定頻率以下的函數近似阶跃函数來表示，結果會得到正弦積分。可以用和Sinc函数的卷積來表示，在信號處理中，這是低通滤波器。

信号处理

（圖下方的）过冲，是因為用非銳化濾鏡來銳化影相所造成

正弦積分是理想低通濾波器的階躍響應

Sinc函数是理想低通濾波器的冲激响应

更多信息：振鈴效應

信号处理中的过冲是指一濾波器輸出的最大值比輸入的最大值大，特別是針對階躍響應，而且經常會伴隨振鈴效應。

像是用Sinc滤波器（例如用矩形低通滤波器）就會出現過沖的情形，其階躍響應為正弦積分

其过沖及下沖可以用這個方式來說明：一般變換的核函數會經過正規化，使其積分為一，因此將常數函數轉換會得到原常數函數，不會有額外的增益。在某一點的卷積是輸入信號的线性组合，再以核函數的值為其（加權）係數。若核函數沒有負值（例如高斯函数），則濾波後信號的數值會是輸入信號的凸组合（核函數積分為一，而且數值非負），因此會在最大值和最小值之間，此值不會有過沖也不會有下沖。不過若核函數有負值（例如Sinc函数），濾波後信號的數值會是輸入信號的仿射組合，輸出數值就可能在輸入信號的最大值及最小值以外，因此會有過沖及下沖的情形。

一般來說过沖是不好的，尤其是會造成削波的情形下，不過有時若要銳化影像，會需要过沖，因為會增加锐度。

相关概念

与过冲非常相关的是振铃，它紧随过冲发生，信号会跌落到低于稳态值，然后可能会反弹到高于稳态，这个过程可能持续一段时间，直到稳定接近于稳态。振铃持续的时间也叫做安定时间。

在社会生态学中，有类似的过冲的概念，是指人口数超过系统的承受容量。

参见

• 阶跃响应
• 振铃
• 安定时间
• 阻尼
• 積分飽和