物理光学

物理光學(英語:physical optics),又稱波動光學(wave optics)是光學的一個分支,研究的是關於干涉、衍射、偏振與其它在幾何光學裏射線近似不成立的種種現象。假設光波的波長超小於儀器的尺寸,能取波長趨向於零的極限為近似,則可以使用幾何光學的方法來解析問題;對於小尺寸儀器,必须假設光波具有有限波長,改使用物理光學的方法來解析問題。[1]:36, 149
在光學通信(optical communication)裏,像量子噪音(quantum noise)一類的效應是包括在干涉理論(coherence theory)的研究領域,通常不會包括在物理光學的研究領域。
物理光學建立在惠更斯原理的基礎上,可以計算複波前(包括振幅与相位)通过光学系统的模型。这一技术能够利用计算机数值仿真模拟或计算衍射、干涉、偏振、像差等各种複杂光学现象。由於仍然會用到近似,物理光学不能像电磁波理论模型一樣地能够全面描述光传播。对于大多数实际问题来说,完整电磁波理论模型需要的计算量太大,在现在的一般计算机硬件条件下并不十分实用,但小尺度的问题可以使用完整波动模型进行计算。
物理光學近似
[编辑]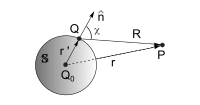
物理光學也是一種近似的前綴,時常引用於光學、電機工程學、應用物理學。對於這上下文,它屬於一種處於忽略波動效應的幾何光學與精確波動理論的電磁學之間的中間方法。在「物理光學」這術語裏,「物理」兩個字的意味著它是比幾何光學更偏向物理方面的理論,而不是一門精確波動理論。[2]:11-13
這種近似應用幾何光學來估算在曲面位置的場,然後積分這場於整個曲面,這樣,可以計算出在任意位置的透射場或散射場。例如,這種近似估算在透鏡、鏡子、孔徑表面的場,然後積分這場於整個表面來計算透射場或散射場。這方法很類似玻恩近似,問題的細節被當作微擾來處理。
在光學裏,這是一種標準地估算衍射效應的方法。由於這是一種高頻率近似,波長越小,估算結果的準確性越高。
物理光學的標準理論對於估算散射場存在有瑕疵,因此,越偏離鏡面方向,準確度越低。[3]2004年,物理學者提出改良理論,能夠計算導體的散射場,並且對於相關問題給出精確解。[4]
參閱
[编辑]參考文獻
[编辑]- ^ Hecht, Eugene, Optics 4th, United States of America: Addison Wesley, 2002, ISBN 0-8053-8566-5 (英语)
- ^ Pyotr Ya. Ufimtsev. Fundamentals of the Physical Theory of Diffraction. John Wiley & Sons. 9 February 2007. ISBN 978-0-470-10900-7.
- ^ Shijo, T.; Rodriguez, L.; Ando, M. The modified surface-normal vectors in the physical optics. Antennas and Propagation, IEEE Transactions on. Dec 2008, 56 (12): 3714–3722. Bibcode:2008ITAP...56.3714S. doi:10.1109/TAP.2008.2007276.
- ^ Umul, Y. Z. Modified theory of physical optics. Optics Express. October 2004, 12 (20): 4959–4972. Bibcode:2004OExpr..12.4959U. PMID 19484050. doi:10.1364/OPEX.12.004959.
- A double-edge-diffraction Gaussian-series method for efficient physical optics analysis of dual-shaped-reflector antennas. Antennas and Propagation. August 2005: 2597.
- Asvestas, J. S. The physical optics method in electromagnetic scattering. Journal of Mathematical Physics. February 1980, 21 (2): 290–299. Bibcode:1980JMP....21..290A. doi:10.1063/1.524413.
